摘要：实际的反卷积会使卷积过程恢复。转置卷积层执行常规卷积，但恢复其空间变换。转换卷积，没有填充，步幅为，内核为转置卷积不会这样做。在神经网络中，我们通常使用称为深度可分离卷积的东西。
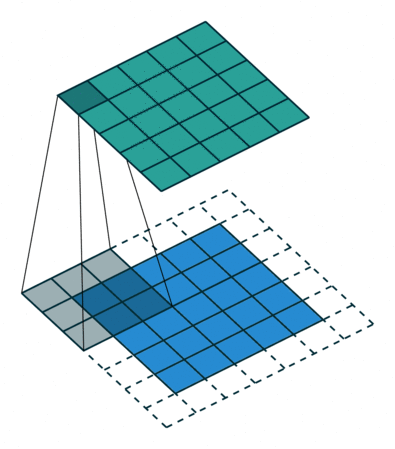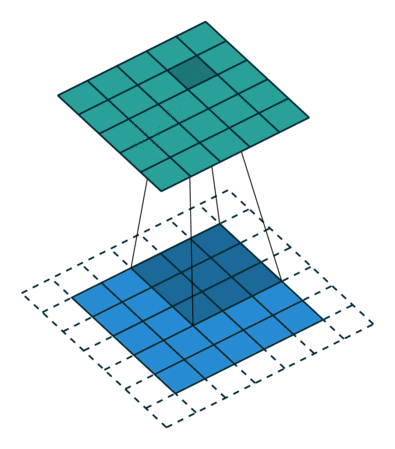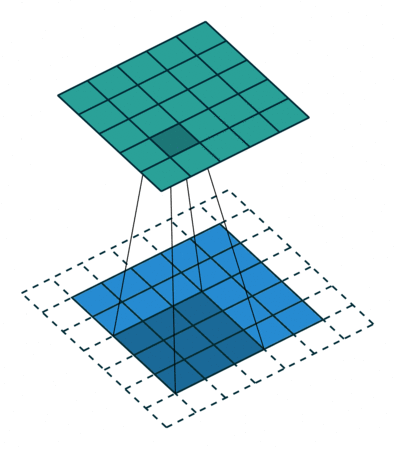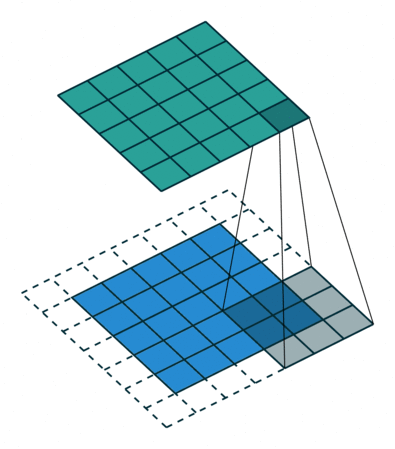
使用内核大小为3，步长为1和填充的2D卷积
一般卷积
首先，我们需要就定义卷积层的一些参数达成一致。
卷积核大小（Kernel Size）：卷积核定义了卷积的大小范围，二维卷积核最常见的就是 3*3 的卷积核。
步长（Stride）：步长定义了当卷积核在图像上面进行卷积操作的时候，每次卷积跨越的长度。在默认情况下，步长通常为 1，但我们也可以采用步长是 2 的下采样过程，类似于 MaxPooling 操作。
填充（Padding）：卷积层采用一定数量的输入通道（I），并且设计特定数量的输出通道（O）。每一层所需的参数可以通过 I*O*K 来进行计算，其中 K 等于卷积核的数量。
输入和输出管道（Input & Output Channels）：卷积层采用一定数量的输入通道
扩张的卷积
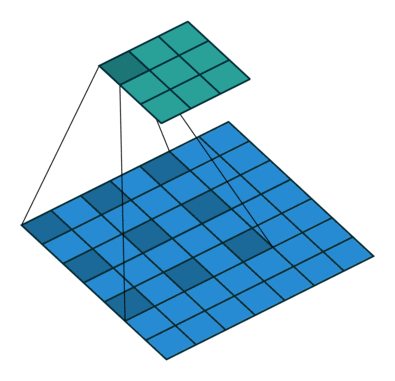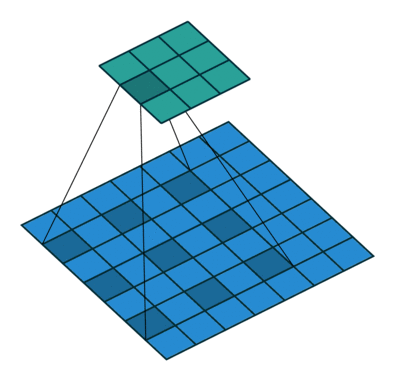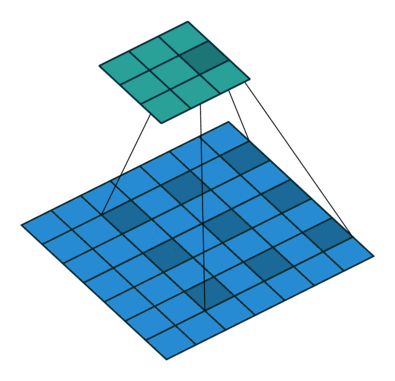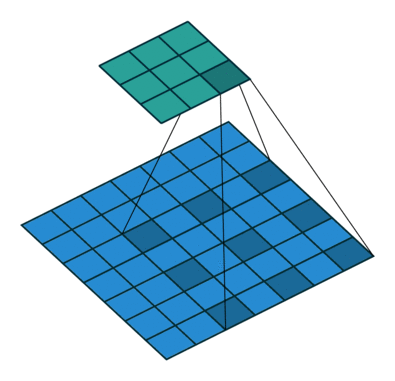
使用3内核进行2D卷积，扩展率为2且无填充
扩张的卷积为卷积层引入另一个参数，称为扩张率。这定义了卷积核中值之间的间距。扩张率为2的3x3内核与5x5内核具有相同的视野，而仅使用9个参数。想象一下，获取一个5x5内核并删除每一个第二列和第二行（间隔删除），就是我们介绍的卷积。
这以相同的计算成本提供了更宽的视野。扩张卷积在实时分割领域中特别受欢迎。如果您需要广泛的视野并且无法承受多个卷积或更大的核，请使用它们。
转置卷积
（又称解卷积或分数跨度卷积）
有些消息来源使用名称deconvolution，这是不合适的，因为它不是解卷积。为了使事情更糟，确实存在解卷积，但它们在深度学习领域并不常见。实际的反卷积会使卷积过程恢复。想象一下，将图像输入到单个卷积层中。现在取出输出，将它扔进一个黑盒子里然后再出现原始图像。这个黑盒子进行反卷积。它是卷积层的数学逆。
转置卷积有点类似，因为它产生与假设的反卷积层相同的空间分辨率。但是，对值执行的实际数学运算是不同的。转置卷积层执行常规卷积，但恢复其空间变换。
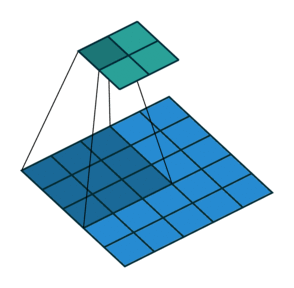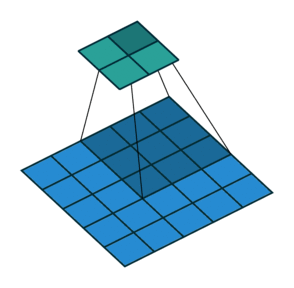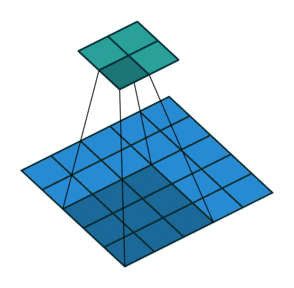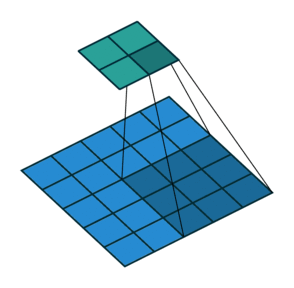
2D卷积，没有填充，步幅为2，内核为3
此时你应该很困惑，让我们看一个具体的例子。将5×5的图像送入卷积层。步幅设置为2，填充停用，内核为3x3。这导致2x2图像。
如果我们想要反转这个过程，我们需要逆数学运算，以便从我们输入的每个像素生成9个值。然后，我们以2的步幅遍历输出图像。这将是反卷积。
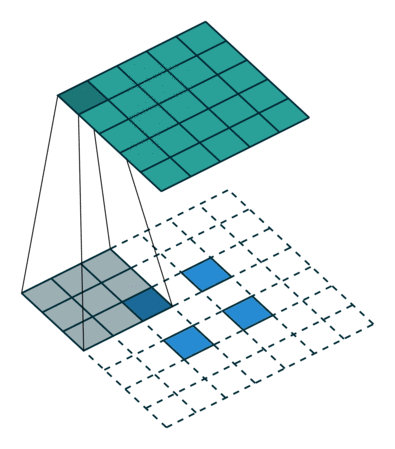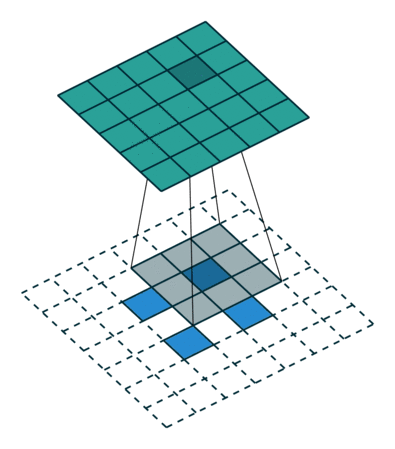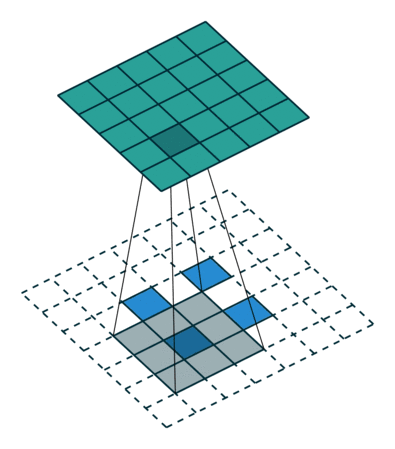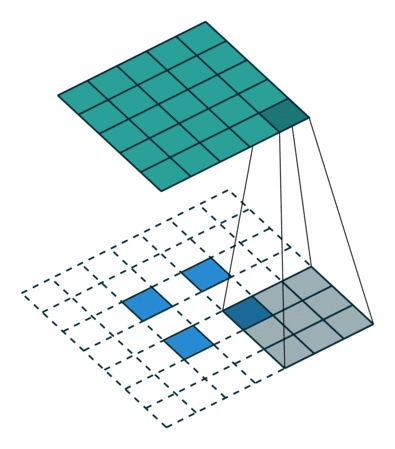
转换2D卷积，没有填充，步幅为2，内核为3
转置卷积不会这样做。的共同点是它保证输出也是5x5图像，同时仍然执行正常的卷积操作。为此，我们需要在输入上执行一些花哨的填充。
正如您现在可以想象的那样，此步骤不会从上面颠倒过程。至少不涉及数值。
它只是从之前重建空间分辨率并执行卷积。这可能不是数学逆，但对于编码器 - 解码器架构，它仍然非常有用。这样我们就可以将图像的升级与卷积相结合，而不是进行两个多带带的处理。
可分离的卷积
在可分离的卷积中，我们可以将内核操作分成多个步骤。让我们将卷积表示为y = conv（x，k），其中y是输出图像，x是输入图像，k是核。简单。接下来，假设k可以通过以下公式计算：k = k1.dot（k2）。这将使它成为可分离的卷积，因为我们可以通过用k1和k2进行2个1D卷积来得到相同的结果，而不是用k进行2D卷积。
Sobel X和Y滤镜
以Sobel内核为例，它通常用于图像处理。你可以通过乘以向量[1,0，-1]和[1,2,1] .T得到相同的内核。在执行相同操作时，这将需要6个而不是9个参数。上面的例子显示了所谓的空间可分卷积，据我所知，它不用于深度学习。
编辑：实际上，通过堆叠1xN和Nx1内核层，可以创建与空间可分离卷积非常相似的东西。这最近在一个名为EffNet的架构中使用，显示了有希望的结果。
在神经网络中，我们通常使用称为深度可分离卷积的东西。这将执行空间卷积，同时保持通道分离，然后进行深度卷积。在我看来，通过一个例子可以较好地理解它。
假设我们在16个输入通道和32个输出通道上有一个3x3卷积层。详细情况是，32个3x3核遍历16个通道中的每个通道，产生512（16x32）个特征映射。接下来，我们通过添加它们来合并每个输入通道中的1个特征图。由于我们可以做32次，我们得到了我们想要的32个输出通道。
对于同一示例中的深度可分离卷积，我们遍历16个通道，每个通道有1个3x3内核，为我们提供了16个特征映射。现在，在合并任何东西之前，我们遍历这16个特征映射，每个特征映射有32个1x1卷积，然后才开始将它们加在一起。这导致656（16x3x3 + 16x32x1x1）参数与上面的4608（16x32x3x3）参数相反。
该示例是深度可分离卷积的特定实现，其中所谓的深度乘数为1.这是迄今为止这种层的最常见设置。我们这样做是因为空间和深度信息可以解耦的假设。看一下Xception模型的表现，这个理论似乎有效。由于其有效使用参数，深度可分离卷积也用于移动设备。
声明：本文版权归原作者所有，文章收集于网络，为传播信息而发，如有侵权，请联系小编及时处理，谢谢！商业智能与数据分析群
兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识
QQ群：81035754
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/4861.html
摘要：目录一引言二轻量化模型三网络对比一引言自年以来，卷积神经网络简称在图像分类图像分割目标检测等领域获得广泛应用。创新点利用和这两个操作来设计卷积神经网络模型以减少模型使用的参数数量。 本文就近年提出的四个轻量化模型进行学习和对比，四个模型分别是：SqueezeNet、MobileNet、ShuffleNet、Xception。目录一、引言 二、轻量化模型 2.1 SqueezeNet ...
摘要：性能在谷歌语音命令数据集上准确率，且参数只有关键字定位是一项旨在检测音频流中预先训练好的单词的任务。其中一个应用就是唤醒词检测。事实上，捕获不同尺度的时间信息是很重要的，因为关键字的特征在时间尺度上通常是不同的。验证集测试集各。 目录 说明 Small-Footprint Keyword S...
阅读 700·2021-11-23 09:51
阅读 878·2021-11-15 17:57
阅读 1484·2021-09-22 15:24
阅读 675·2021-09-07 09:59
阅读 2078·2019-08-29 15:10
阅读 1722·2019-08-29 12:47
阅读 644·2019-08-29 12:30
阅读 2928·2019-08-28 17:46
