摘要：最近老顾收到很多读者来信，绝大多数询问对抗生成网络的最优传输解释，以及和蒙日安培方程的关系。蒙日安培方程的几何解法硬件友好，可以用目前的并行实现。蒙日安培方程的正则性理论更加复杂，但是对于模式塌缩的理解非常关键。
最近老顾收到很多读者来信，绝大多数询问对抗生成网络的最优传输解释，以及和蒙日-安培方程的关系。很多问题涉及到经典蒙日-安培方程理论，这里我们从偏微分方程和几何角度介绍一下蒙日-安培方程的理论，主要是解的存在性，性。我们尽量用较为初等的方式来解释。
深度学习和最优传输
深度学习的巨大成功可以归结为自然数据所满足如下两个定则：1）流形分布律：同类自然数据满足特定的概率分布，可以用概率分布来刻画，其支集是高维数据背景空间中的低维流形；2）聚类分布律：同一数据中的不同子类表示成不同的概率分布；并且这些概率分布之间的距离足够远，使得这些子类可以被区分。因此，深度学习的核心任务包括：1）学习流形结构：即计算从流形到参数域的参数化映射（编码、解码映射）；也计算流形之间的映射；2）概率分布变换：在特征空间或者图像空间中，计算两种概率分布之间的距离，和两种概率分布之间的变换。
基于最优传输观点，特别是几何上的Alexandrov途径，我们设计了新颖的生成模型，进行了初步试验。这里的几何算法可以用硬件加速。详细的讨论请见深度学习和几何（演讲提要）。下面，我们用尽量初等的方法来介绍蒙日-安培方程弱解的存在性和性。
凸函数
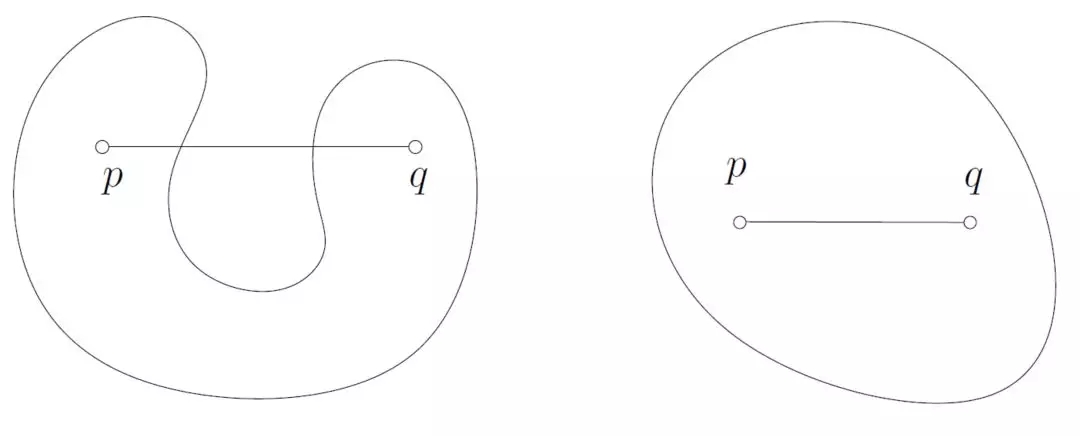
图1. 左帧非凸集，右帧凸集。
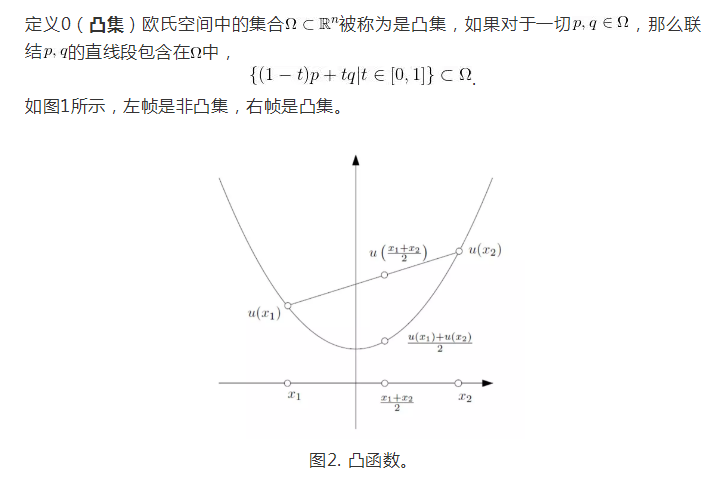
证明基于下面事实：正定矩阵之和、正定矩阵和正常数的数乘还是正定矩阵；或者用第一个定义。
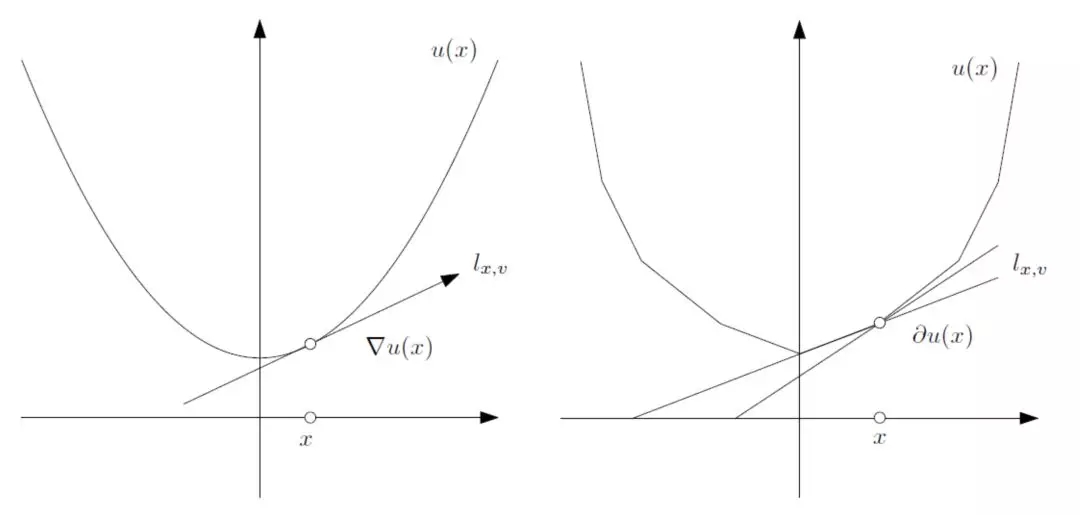
图3. 凸函数的次微分。
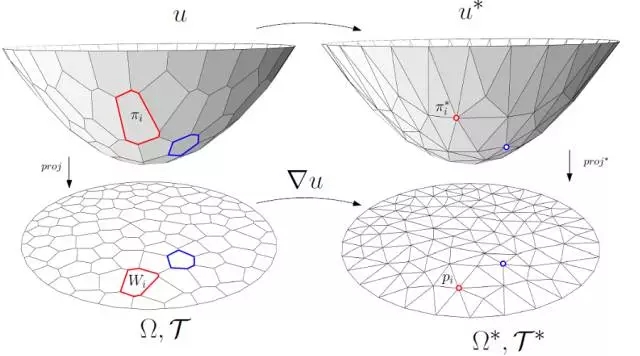
图4. 勒让德变换。
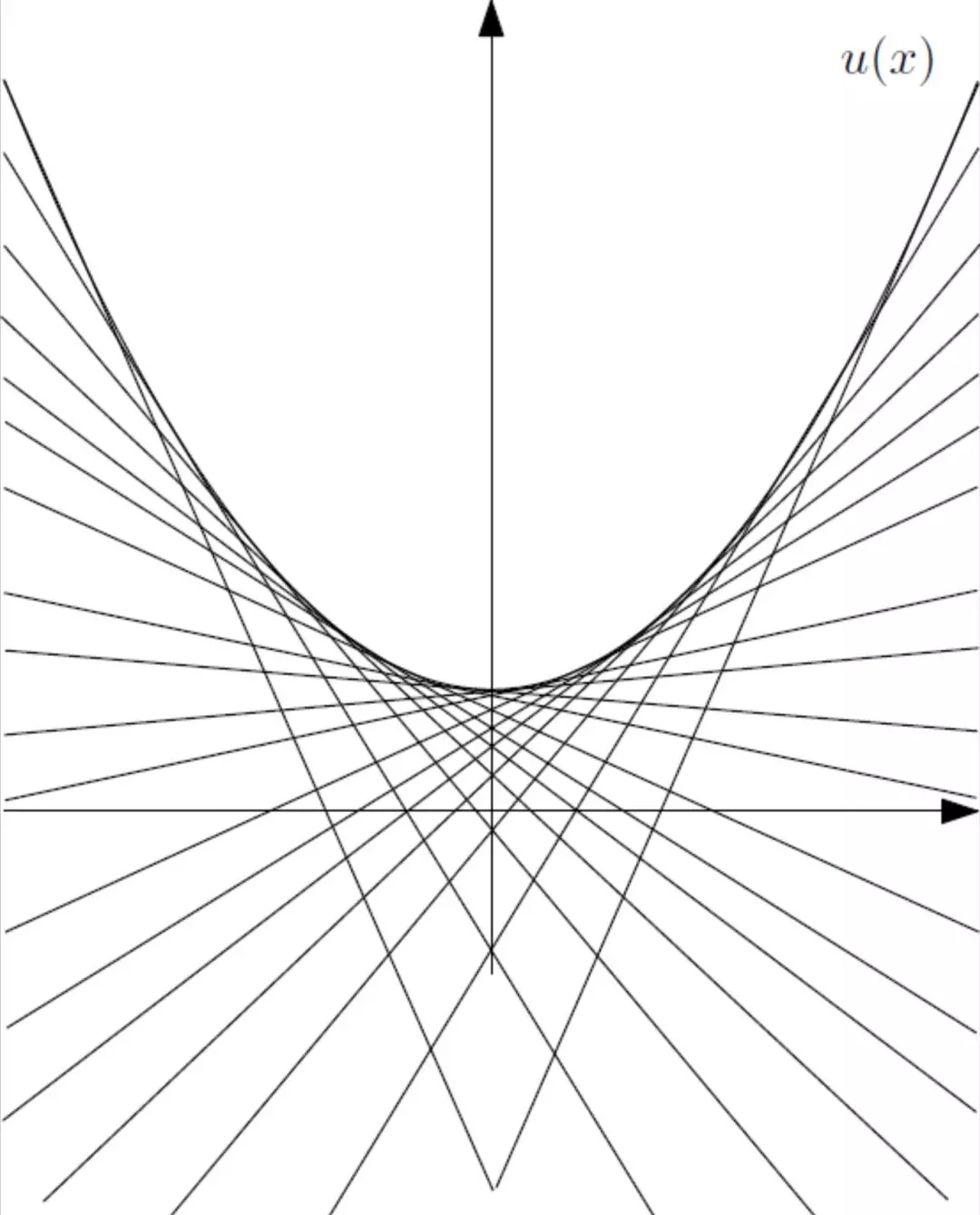
图5. 由支撑平面重构凸函数。
蒙日-安培测度
蒙日-安培测度具有非常直观而且重要的特性。
不等式成立。
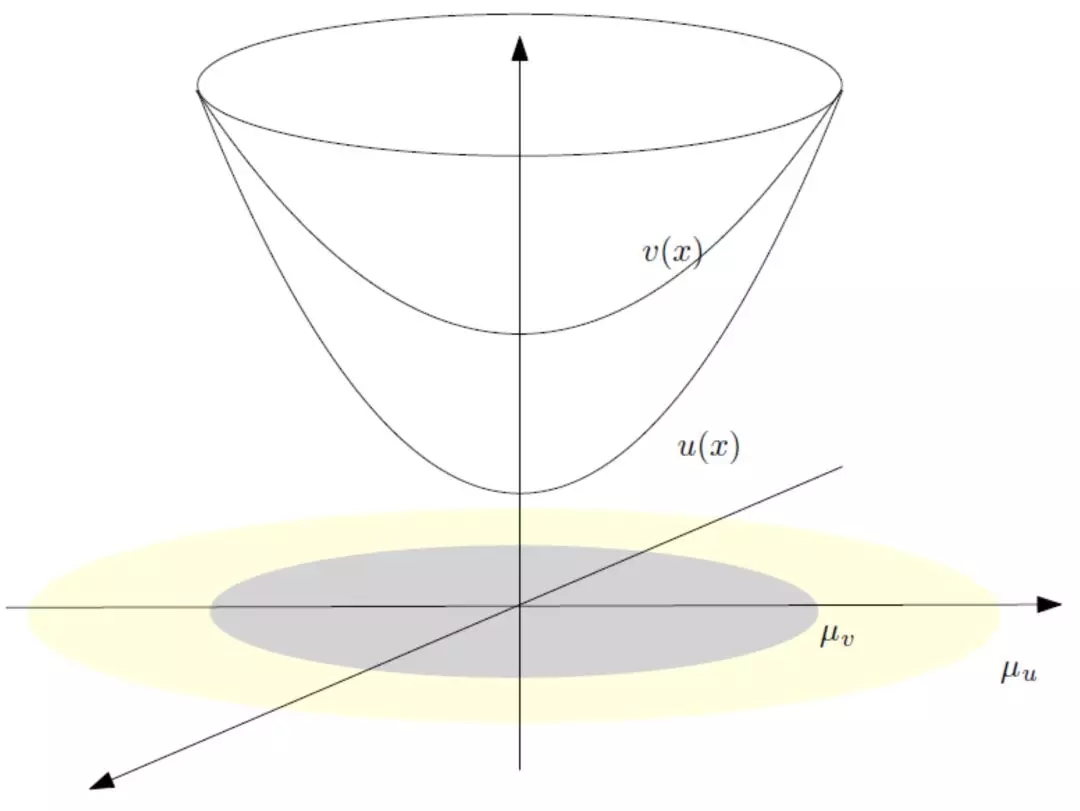
图6. 次微分的单调性。
蒙日-安培方程
我们可以得到迪利克雷问题弱解的稳定性如下：
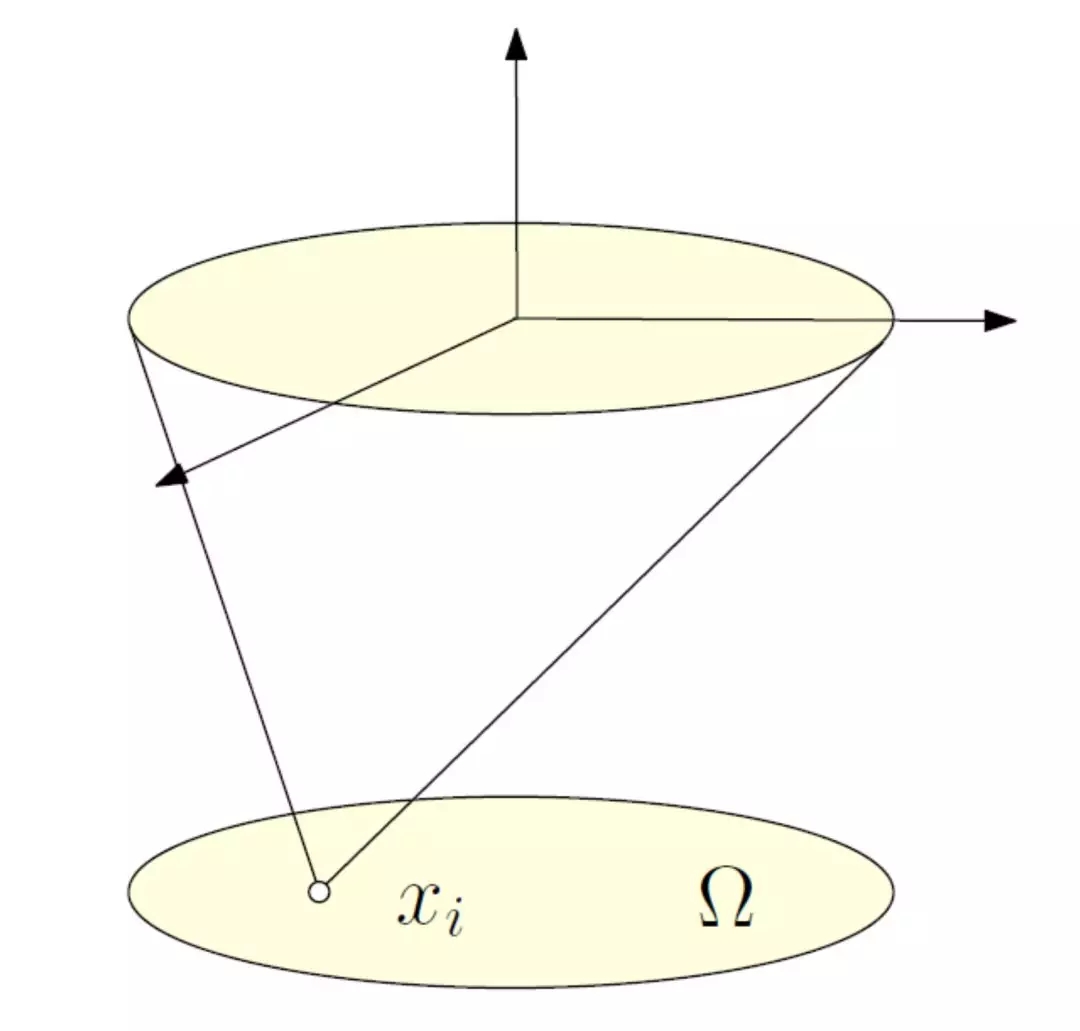
图7. 锥函数。
最优传输映射和蒙日-安培方程
小结
对抗生成模型（GAN model）可以用最优传输理论来解释和计算，生成器等价于求解最优传输映射，判别器等价于计算Wasserstein距离，即最优传输映射的传输总代价。
传输代价的Brenier理论将最优传输映射求解归结为蒙日-安培方程的弱解。这里我们用尽量初等的方法介绍了蒙日-安培方程弱解（Alexandrov 解）的存在性和性，由此帮助大家奠定学习GAN模型的理论基础。
除了理论严密清晰，白箱替代黑箱，从深度学习的实战角度而言，用蒙日-安培方程的几何解法计算最优传输映射来部分替代目前深度神经网络生成模型方法，具有很多优点：
蒙日-安培方程的几何解法归结为凸优化问题，保证最优解的存在性和性，不会停留在局部最优上面；
蒙日-安培方程的几何解法具有明确的海森矩阵，可以用牛顿法进行优化，二阶收敛。或者用超线性的拟牛顿法，效率远高于线性的梯度下降法。
蒙日-安培方程几何解法的误差可以较精确控制，采样密度和逼近Brenier势能函数的
误差模有确定关系，可以自适应条件采样密度，以提高逼近精度。
算法设计具有层级（hirearchical）和自适应（self adaptive）特性，进一步提高效率。
蒙日-安培方程的几何解法硬件友好，可以用目前的GPU并行实现。
实验结果验证了我们的看法，用这种方法从效率和生成质量而言，优于传统方法。
蒙日-安培方程的正则性理论更加复杂，但是对于模式塌缩的理解非常关键。我们会在未来加以详尽讨论。
声明：文章收集于网络，为传播信息而发，如有侵权，请联系小编及时处理，谢谢！
商业智能与数据分析群
兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识
QQ群：81035754
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/4848.html
摘要：我们将这些现象笼统称为广义的模式崩溃问题。这给出了模式崩溃的直接解释。而传统深度神经网络只能逼近连续映射，这一矛盾造成了模式崩溃。 春节前夕，北美遭遇极端天气，在酷寒中笔者来到哈佛大学探望丘成桐先生。新春佳节，本是普天同庆的日子，但对于孤悬海外的游子而言，却是更为凄凉难耐。远离父母亲朋，远离故国家园，自然环境寒风凛冽，飞雪漫天，社会环境疏离淡漠，冷清寂寥。在波士顿见到导师和朋友，倍感欣慰。笔...
摘要：老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告，汇报了这方面的进展情况。深度学习的主要目的和功能之一就是从数据中学习隐藏的流形结构和流形上的概率分布。 （最近，哈佛大学丘成桐先生领导的团队，大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告，汇报了这方面的进展情况。这里是报告的简要记录，具体内容见【1...
摘要：在最近的一次人工智能会议上，表示自己对于反向传播非常怀疑，并提出应该抛弃它并重新开始。在人工智能多年的发展过程中，反向传播已经成为了深度学习不可或缺的一部分。最后，我们会将这些规则组合成可用于任意神经网络的反向传播算法。 现在的深度学习发展似乎已经陷入了大型化、深度化的怪圈，我们设计的模型容易被对抗样本欺骗，同时又需要大量的训练数据——在无监督学习上我们取得的突破还很少。作为反向传播这一深度...
摘要：因为深度学习的正统观念在该领域已经很流行了。在机器和深度学习空间中进行的大多数数学分析倾向于使用贝叶斯思想作为参数。如果我们接受了目前深度学习的主流观点任何一层的微分都是公平的，那么或许我们应该使用存储多种变体的复分析。 深度学习只能使用实数吗？本文简要介绍了近期一些将复数应用于深度学习的若干研究，并指出使用复数可以实现更鲁棒的层间梯度信息传播、更高的记忆容量、更准确的遗忘行为、大幅降低的网...
阅读 1818·2019-08-30 15:55
阅读 1010·2019-08-26 11:57
阅读 513·2019-08-26 11:29
阅读 3361·2019-08-26 10:49
阅读 1911·2019-08-23 18:40
阅读 1751·2019-08-23 16:04
阅读 3108·2019-08-23 11:01
阅读 2273·2019-08-23 10:56
