训练神经网络的最快方法：Adam优化算法+超级收敛

摘要：在实践中，几乎总是通过向梯度增加来实现算法，而不是真正改变损失函数。显然这是两种不同的方法。那么，权重衰减是不是总比的正则化更好呢我们还没发现明显更糟的情况，但无论是迁移学习问题例如斯坦福汽车数据集上的的微调还是

跌宕起伏的 Adam

纵观 Adam 优化器的发展历程，就像过山车一样。它于 2014 年在论文 Adam: A Method for Stochastic Optimization（https://arxiv.org/abs/1412.6980 ）中首次提出，其核心是一个简单而直观的想法：既然我们明确地知道某些参数需要移动得更快、更远，那为什么每个参数还要遵循相同的学习率呢？因为最近梯度的平方告诉我们每增加一个权重可以得到多少个信号，所以我们可以除以它来确保即使是最缓慢的权重也能获得“发光”的机会。Adam 接受了这个想法，在过程中增加了标准方法，Adam 优化器就这样诞生了。它需要稍微调整来避免早期批出现偏差。

当论文首次发布时，原论文中的一些图表（如下图所示）让深度学习社区感到兴奋不已：

Adam 和其他优化器的对比

训练速度加快了 200%！

“总体来看，我们发现 Adam 非常强大，非常适用于时下机器学习领域中的各种非凸优化问题。”论文如此总结道。那是三年前深度学习最辉煌的时候。但事情后来并没有像我们所期望的那样发展，很少见到有研究文章使用 Adam 来训练模型，新的研究也开始明显地不鼓励使用 Adam（如论文 The Marginal Value of Adaptive Gradient Methods in Machine Learning，https://arxiv.org/abs/1705.08292 ），并通过几个实验结果表明，普通的 SGD+Momentum 可能比复杂的 Adam 表现更好。在 2018 年 fast.ai 的课程中，可怜的 Adam 就被从早期课程中剔除了。

但在 2017 年底，Adam 似乎获得了重生。Ilya Loshchilov 和 Frank Hutter 在他们的论文 Fixing Weight Decay Regularization in Adam（https://arxiv.org/abs/1711.05101 ）中指出，在每个库中在 Adam 上实施的权重衰减似乎都是错误的，并提出了一种简单的方法（他们称之为 AdamW）来修复这个问题。虽然他们的结果略有不同，但是他们确实给出了一些令人鼓舞的图表，如下图所示：

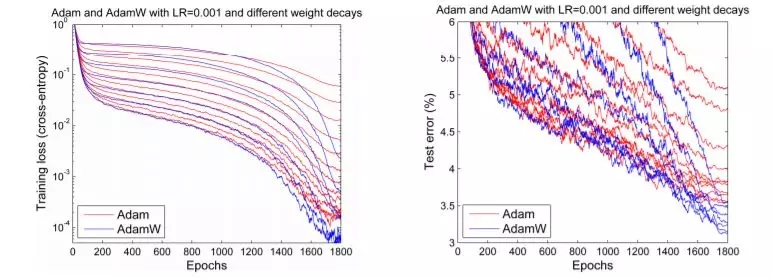
Adam 和 AdamW 对比

我们期待人们能够对 Adam 重燃热情，因为它的一些早期结果似乎已经可以重现。但事实并非如此。应用它的一个深度学习框架是 fastai，使用的是 Sylvain 编写的代码。但因为缺乏可用的通用框架，日常实践者就被又旧又难用的 Adam 所困。

但这并不是问题，前方还有更多的障碍。有两篇论文分别指出了 Adam 在收敛性证明方面存在明显的问题。尽管其中一篇论文提出了解决方案（并在久负盛名的 ICLR 大会上获得了“较佳论文”奖），他们称之为_AMSGrad_。但是，如果要说我们从这段充满戏剧化的生活（至少按照优化器的标准而言是戏剧化的）中学到了什么，那就是，没有什么是表面看到的那样。事实上，博士生 Jeremy Bernstein 在博文 On the Convergence of Adam and Beyond（https://openreview.net/forum?id=ryQu7f-RZ¬eId=B1PDZUChG ）中指出，所谓的收敛问题实际上只是超参数选择不当，也许 AMSGrad 并不能解决问题。另一名博士生 Filip Korzeniowski 在论文 Experiments with AMSGrad（https://fdlm.github.io/post/amsgrad/ ） 中展示了一些早期研究成果，似乎也证明了这个令人沮丧的观点。

Adam 到底怎么样？

对于那些只想快速训练较精确模型的人，我们该做些什么呢？让我们用数百年来解决科学辩论的方式来解决这一争议：做实验！

我们将在本文稍后阐述所有的细节，但先让我们看一下大致结果：

适当调参之后，Adam 真的是能用的！我们在各种任务上获得了训练时间方面的结果如下：

在含有测试时间增加的 18 个 epoch 或 30 个 epoch 训练 CIFAR10，使其准确率超过 94%，如 DAWNBech 竞赛；

只需 60 个 epoch 即可对 Resnet50 进行调参，使其在斯坦福汽车数据集的准确率达到 90%，据报告称，之前要达到相同的准确率需 600 个 epoch；

从零开始训练 AWD LSTM 或 QRNN（见论文 Regularizing and Optimizing LSTM Language Models，https://arxiv.org/abs/1708.02182 ），需 90 个 epoch（或在单个 GPU 上训练一个半小时），其困惑度在 Wikitext-2 达到当前最优水平，据之前报告称，LSTM 需要 750 个 epoch，QRNN 需要 500 个 epoch。

这意味着我们已经看到了使用 Adam 的超收敛！（参见论文 Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates，https://arxiv.org/abs/1708.07120 ）超收敛是训练学习率高的神经网络时出现的一种现象，表示节约了一半的训练时间。在人们了解 AdamW 之前，人们训练 CIFAR10 使其准确率达到 94% 需要大约 100 个 epoch。

与之前的工作相比，我们发现只要调整得当，Adam 在尝试过的每一个 CNN 图像问题上都能获得与 SGD+Momentum 一样的准确率，而且，几乎总是快一点。

至于有人认为 AMSGrad 是一个槽糕的“解决方案”，这种看法是正确的。我们一直发现，AMSGrad 的准确率（或其他相关指标）并没有获得比普通的 Adam/AdamW 更高的增益。

如果你听到人们说 Adam 的泛化性能不如 SGD+Momentum 时，你基本就会发现他们为自己的模型选择的超参数其实蛮糟糕的。通常情况下，Adam 需要比 SGD 更多的正则化，因此，当从 SGD 转向到 Adam 时，一定要确保调整正则化超参数。

AdamW

理解 AdamW：权重衰减与 L2 正则化

L2 正则化是减少过拟合的经典方法，它向损失函数添加模型的所有权重的平方和组成的惩罚项，乘以特定的超参数来控制惩罚力度（在本文中，所有的方程式均使用 Python、NumPy 和 PyTorch 表示法）：

final_loss = loss + wd * all_weights.pow(2).sum() / 2

其中，wd是我们设置的超参数，也可称为权重衰减，因为运用 vanilla SGD 时，它相当于使用如下方程式更新权重：

w = w - lr * w.grad - lr * wd * w

其中，lr表示学习率，w2表示损失函数对w的导数，wd*w表示惩罚项对w的求导结果。在这个方程式中，我们可以看到每一次更新都会减去一小部分权重，因此这就是命名为“衰减”的原因。

我们注意到所有的库都使用了第一种形式。在实践中，几乎总是通过向梯度增加wd*d来实现算法，而不是真正改变损失函数。因为我们不希望还有其他更简单的方法的情况下，增加额外的计算量来修正损失。

如果这两个概念是一样的话，那为什么还要区分这两种概念呢？答案就是，它们对于 vanilla SGD 来说是等价的，一旦我们添加动量，或者使用像 Adam 那样复杂的最优化器，那么 L2 正则化（第一个方程式）和权重衰减（第二个方程式）就会变得不同。在本文其余部分中，我们讨论的权重衰减都是指第二个方程式（权重将会衰减一点），而我们讨论经典方法时就会讨论 L2 正则化。

让我们来看看带动量的 SGD。使用 L2 正则化会在梯度上添加wd*d（正如我们前面所述），但梯度并不是直接从权重中减去。首先我们要计算一个移动均值：

moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)

这个移动均值乘以学习率，再减去w得到权重的更新，因此w与正则化相关的部分是lr*(1-alpha)*wd*d加上已经在moving_avg中前面权重的结合。

因此，权重衰减的更新方式可以如下表示：

moving_avg = alpha * moving_avg + (1-alpha) * w.grad 

w = w - lr * moving_avg - lr * wd * w

我们可以看到，从w连接到正则化的部分在两种方法是不一样的。在使用 Adam 优化器时，权重衰减的部分可能相差很大：在 L2 正则化的情况下，我们将这个wd*d添加到梯度中，然后分别计算梯度机器平方的移动均值，然后再更新权重。然而权重衰减方法只是简单地更新权重，然后每次从权重中减去一点。

显然这是两种不同的方法。在进行实验之后，Ilya Loshchilov 和 Frank Hutter 在论文中建议我们应该使用 Adam 的权重衰减方法，而不是像经典深度学习库中实现的 L2 正则化方法。

实现 AdamW

那我们要怎么做才能实现 AdamW 呢？如果你在使用 fastai 库，那么在使用 fit 函数时只需添加参数use_wd_sched=True就能简单地实现了：

learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)

如果你更青睐新的训练 API，那你可以在每个训练阶段中使用参数wd_loss=False（用于在衰减过程中没有计算的权重衰减）：

phases = [TrainingPhase(1, optim.Adam, lr, wds=1-e4, wd_loss=False)]

learn.fit_opt_sched(phases)

以下是我们在 fastai 中如何实现 AdamW 的简要总结。在优化器中的阶跃函数（step function）中，只需使用梯度修正参数，根本不使用参数本身的值（除了权重衰减，我们将在外部处理）。我们可以在最优化器步骤之前通过简单的实现权重衰减，但这仍然需要在计算梯度之后才能完成，否则会影响梯度值。因此在训练循环中，我们必须确定计算权重衰减的位置。

loss.backward()

#Do the weight decay here!

optimizer.step()

当然，最优化器应该设定为 wd=0，否则它还会做一些 L2 正则化，这也是我们不希望看到的。现在在权重衰减的位置中，我们可以在所有参数上进行循环，并依次采用权重衰减的更新。我们的参数应该存储在优化器的字典param_groups中，因此这个循环应该如下段代码所示那样的：

loss.backward()

for group in optimizer.param_groups():

   for param in group["params"]:

       param.data = param.data.add(-wd * group["lr"], param.data)

optimizer.step()

AdamW 实验结果：是否有效？

我们先在计算机视觉问题上进行了测试，结果令人鼓舞。具体来说，我们使用 Adam 和 L2 正则化在 30 个 epoch（这是 SGD 在 1cycle 策略（详见 https://sgugger.github.io/the-1cycle-policy.html）中达到 94% 准确率的必要时间）获得的准确率平均为 93.36%，在两次中有一次超过了 94%。当使用 Adam 和权重衰减方法时，我们始终得到的是 94%~94.25% 的准确率。为此，我们发现使用 1cycle 策略时，beta2 的最优值为 0.99。我们将 beta1 参数作为 SGD 的动量，也就是说，随着学习率的增长，它从 0.95 降到 0.85，然后随着学习率的降低又升到 0.95。

L2 正则化或权重衰减准确率

更令人印象深刻的是，使用测试时间增加（即对测试集的一个图像和它的四个数据增强版本进行预测的平均值），我们可以在仅仅 18 个 epoch 内达到 94% 的准确率（平均 93.98%）！使用简单的 Adam 和 L2 正则化的话，每尝试 20 个 epoch 就会出现一次超过 94% 的情况。

在这些比较中需要考虑的一件事是，改变正则化的方式会改变权重衰减或学习率的较佳值。在我们进行的测试中，L2 正则化的较佳学习率为 1e-6（较大学习率为 1e-3），而 0.3 是权重衰减的较佳值（学习率为 3e-3）。在我们的测试中，数量级的差异都是非常一致的，主要是因为 L2 正则化被梯度的平均范数（相当低）有效地划分，并且 Adam 的学习率相当小（所以权重衰减的更新需要更强的系数）。

那么，权重衰减是不是总比 Adam 的 L2 正则化更好呢？我们还没发现明显更糟的情况，但无论是迁移学习问题（例如斯坦福汽车数据集上的 Resnet50 的微调）还是 RNN，它都没有给出更好的结果。

AMSGrad

理解 AMSGrad

AMSGrad 是由 Sashank J. Reddi、Satyen Kale 和 Sanjiv Kumar 在最近的一篇文章 On the Convergence of Adam and Beyond（https://openreview.net/forum?id=ryQu7f-RZ ）中介绍的。通过分析 Adam 优化器的收敛性证明，他们发现了更新规则中的一个错误，该错误可能导致算法收敛到次优点。他们设计了理论实验，展示了 Adam 失败的情形，并提出了一个简单的解决方案。

为了更好地理解错误和解决方案，让我们看一下 Adam 的更新规则：

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad

avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)

w = w - lr * avg_grads / sqrt(avg_squared)

我们刚刚跳过了偏差修正（这对训练的开始很有用) 来关注重点。作者发现的 Adam 收敛性证明中的错误之处在于它需要数量。

lr / sqrt(avg_squared）

这是我们朝着平均梯度方向迈出的一步，在训练中逐渐减少。由于学习率通常是常量或递减的（除了像我们这样疯狂的人试图获得超收敛之外），作者提出的解决方案是通过添加另一个变量来跟踪它们的较大值来迫使avg_square量增加。

实现 AMSGrad

相关文章在 ICLR 2018 中获得了一项大奖，并已经在两个主要的深度学习库——PyTorch 和 Keras 中实现了。所以我们只要传入参数amsgrad=True就万事大吉了。

前一节中的权重更新代码更改为如下内容:

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad

avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)

max_squared = max(avg_squared, max_squared)

w = w - lr * avg_grads / sqrt(max_squared)

AMSGrad 实验结果：大量毫无意义的噪音

AMSGrad 的表现令人失望。我们发现，在所有的实验中，它一点用都没有。即使 AMSGrad 发现的最小值确实有时比 Adam 达到的最小值略低（在损失方面），其度量（准确率、f1 分数等）最终总是更槽糕（请访问此网址参阅更多表格和示例：https://fdlm.github.io/post/amsgrad/ ）

Adam 优化器在深度学习中收敛的证明（因为它是针对凸问题的）和他们在其中发现的错误对于与现实问题无关的合成实验很重要。实际的测试表明，当那些avg_squared梯度想要减少时，这样做能得到较好的结果。

这表明，即使对理论的关注对获得一些新想法很有用，也没有什么能代替实验（以及大量的实验），以确保这些想法能够帮助实践者训练更好的模型。

附录: 全部结果

从零开始训练 CIFAR10（模型是一个 WideResnet 22，如下表所示为五个模型的测试集中平均误差结果）：

使用 fastai 库引入的标准头对斯坦福汽车数据集上的 Resnet50 进行微调（在解冻前对头进行 20 个 epoch 的训练，并用不同的学习率训练 40 个 epoch）：

使用 github repo 中的超参数（https://github.com/salesforce/awd-lstm-lm ）对 AWD LSTM 进行训练（结果显示在有无缓存指针的情况下验证 / 测试集的困惑度）：

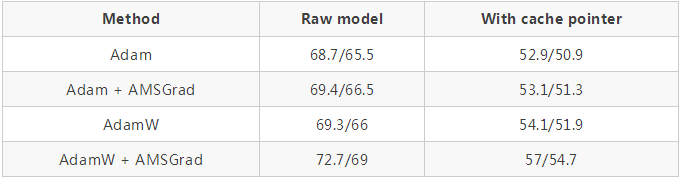
QRNNs 代替 LSTMs 也一样：

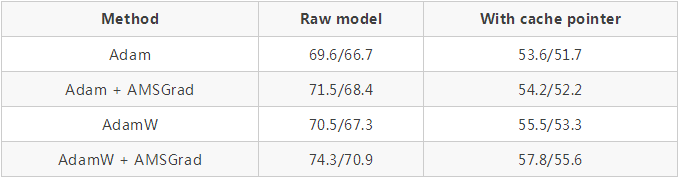
对于这个特定的任务，我们使用了一个改进版本的 1cycle 策略，加快了学习速度，之后长时间保持较高的恒定学习速度，然后再次下降。

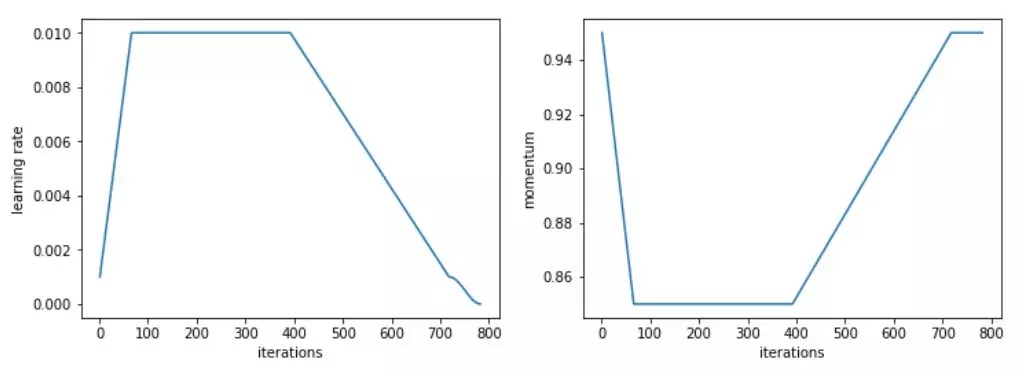
Adam 和其他优化器之间的对比

所有相关超参数的值以及用于生成这些结果的代码可访问此网址来获得：

https://github.com/sgugger/Adam-experiments

原文链接：

AdamW and Super-convergence is now the fastest way to train neural nets

http://www.fast.ai/2018/07/02/adam-weight-decay/

声明：文章收集于网络，如有侵权，请联系小编及时处理，谢谢！

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754