资讯专栏INFORMATION COLUMN

摘要:老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告,汇报了这方面的进展情况。昨天年月日,严东辉教授邀请老顾在泛华统计协会举办的应用统计会议上做了深度学习的几何观点的报告。小结最优传输理论可以用于解释深度学习中的概率分布变换。
(最近,哈佛大学丘成桐先生领导的团队,大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为“深度学习的几何观点”的报告,汇报了这方面的进展情况。这里是报告的简要记录,具体内容见【1】。)
昨天(2018年6月15日),严东辉教授邀请老顾在泛华统计协会( International Chinese Statistical Association)举办的应用统计会议(ICSA2018 Applied Statistics Symposium)上做了“深度学习的几何观点”的报告。会议上Eric Xing教授给出报告,用统计概率的观点统一了变分自动编码器(VAE,Variational Autoencoder)和生成对抗网络(GAN,Generative Aderseral Network)。老顾用几何观点将VAE和GAN加以分析,再度阐述GAN模型中的对抗是虚拟的,没有必要的,生成器网络和判别器网络是冗余的。(以前的博文曾经系统阐述过,请见 “虚构的对抗,GAN with the wind”)下面我们从几何角度详细解释。
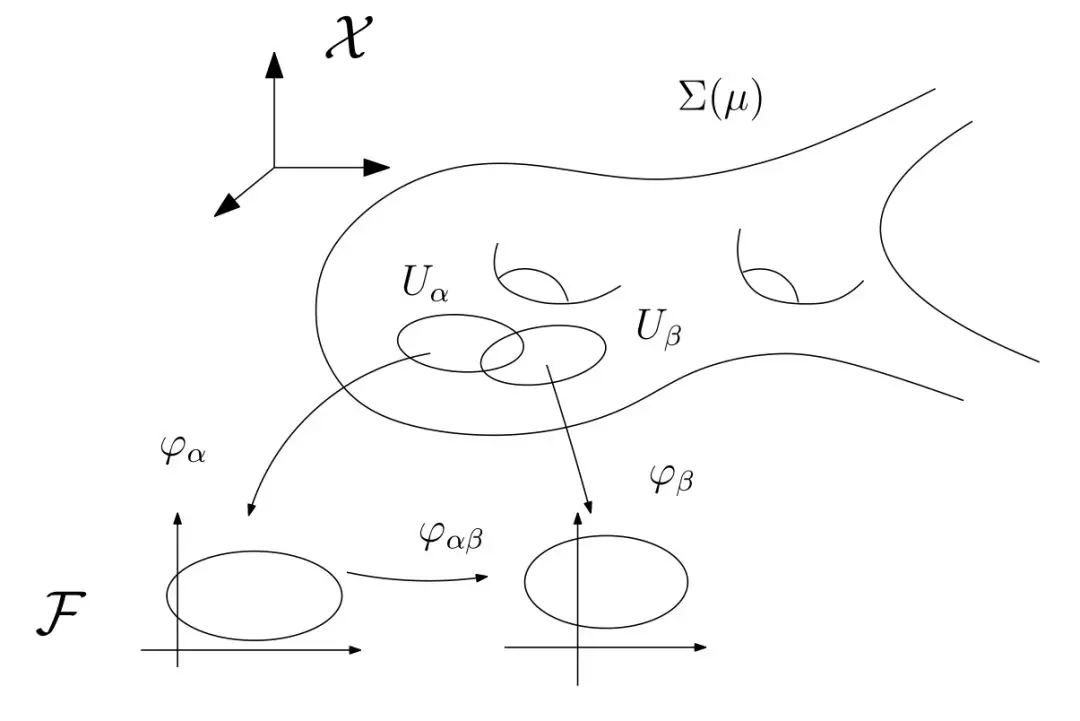
图1. 流形结构。
我们前面阐述过深度学习成功的核心原因可以部分归结为流形分布律和聚类分布律(深度学习的几何观点(1) - 流形分布定律),深度学习的基本任务就在于从数据中学习流形结构,建立流形的参数表达;和变换概率分布。



图2. 隐空间的同胚映射,改变概率分布。



凸几何理论
最优传输的理论天然地和凸几何闵可夫斯基理论等价,因此我们可以用更为直观的几何观点来分析概率变换问题,从而可以将深度学习中的黑箱部分用透明的数学模型来取代。
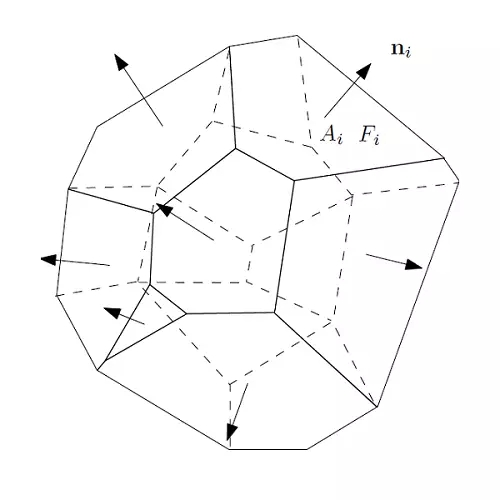
图3. 闵可夫斯基定理。
如图3所示,给定一个凸多面体,每个面的法向量已知,面积已知,所有面的面积和法向量的乘积之和等于0,闵可夫斯基(Minkowski)定理证明这样的凸多面体存在,并且彼此相差一个平移。
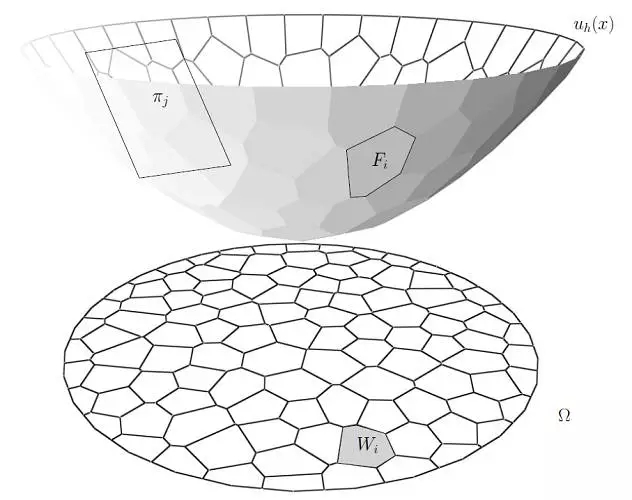
图5. 亚历山大定理。

这一理论可以直接推广到任意维,证明不需要改动。
Brenier理论,Alexandroff理论的等价关系
最优传输的Brenier理论和凸几何的Alexandroff理论本质上是等价的。下面我们来具体分析。
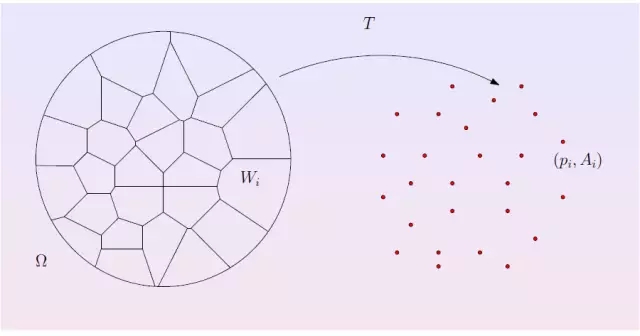
图6. 离散最优传输问题。


图7. 离散Brenier势能函数的构造。



图6. 最优传输映射的计算实例。
图6显示了这种方法的一个计算实例,首先我们将滴水兽曲面用黎曼映照映射到平面单位圆盘,黎曼映射的像如下行左帧所示,那么曲面的面元诱导了平面圆盘上的一个测度。平面圆盘上的欧氏面元定义了均匀测度。我们用上面讲述的变分法来构造平面圆盘到自身的最优传输映射,最优传输映射的像如下行右帧所示。那么最优传输映射的结果给出了从曲面到平面圆盘的保面元映射。
对抗生成网络(GAN)
2014年,Goodfellow 提出了GAN的概念,他的解释如下:GAN的核心思想是构造两个深度神经网络:判别器D和生成器G,用户为GAN提供一些真实货币作为训练样本,生成器G生成假币来欺骗判别器D,判别器D判断一张货币是否来自真实样本还是G生成的伪币;判别器和生成器交替训练,能力在博弈中同步提高,最后达到平衡点的时候判别器无法区分样本的真伪,生成器的伪造功能炉火纯青,生成的货币几可乱真。这种计算机左右手互搏的对抗图景,使得GAN成为更为吸引人的深度学习模型。
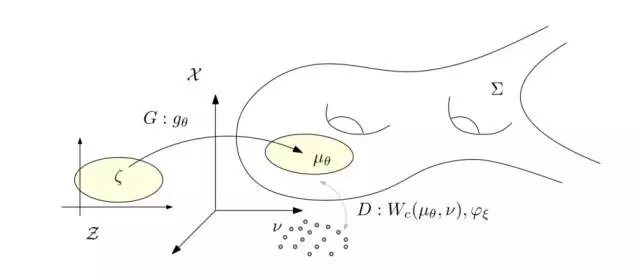
图7. WassersteinGAN的理论框架。


这意味着:在最优情况下,判别器D由生成器G的结果直接给出;生成器G由判别器D的结果直接给出;判别器D和生成器G之间的对抗是虚拟的;判别器网络和生成器网络是冗余的。这和人们对于GAN模型生成器、判别器相克相生的想象大相径庭。
半透明深度网络模型
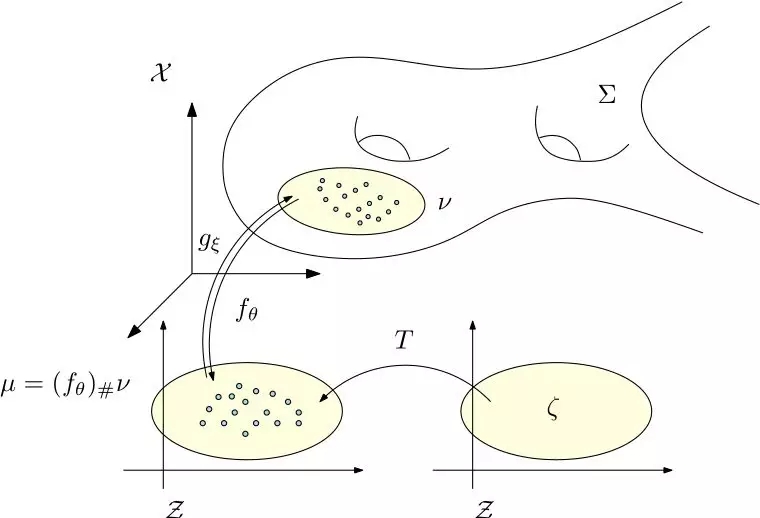
图8. 半透明深度网络模型。
传统的变分自动编码器VAE核心想法是将隐空间的概率分布变换成高斯分布,手法相当曲折。
因为概率变换可以用最优传输理论来清晰阐释,并且用牛顿法优化凸能量可以保证全局最优性,和高阶收敛速度,我们可以将深度学习中的概率变换部分分离出来,用透明的数学模型来取代,其他部分依然用传统的黑箱来运算,如此得到了半透明的网络模型【4】。


real digits and VAE results

WGAN and AE-OMT
图9. 半透明网络的计算结果和其他模型的计算结果比较。
我们将半透明网络做为生成模型,在手写体数据集合上进行测试。如图9所示,半透明网络的计算结果优于传统的VAE和WGAN结果。

图10. VAE和半透明网络比较。
我们将半透明网络做为生成模型,在人脸图片数据集合上进行测试。如图10所示,半透明网络的计算结果优于传统的VAE结果。
小结
最优传输理论可以用于解释深度学习中的概率分布变换。最优传输的Brenier理论和凸几何中的Alexandroff理论等价,我们的理论结果给出了基于变分法的构造。在这种情形下,生成器和判别器彼此等价,它们之间的对抗不再需要,网络体系结构可以大幅简化。在深度学习中,我们可以将流形降维和概率变换分开,用透明的最优传输模型来部分取代黑箱,得到半透明网络模型。
References
Na Lei, Zhongxuan Luo, Shing-Tung Yau and David Xianfeng Gu. "Geometric Understanding of Deep Learning". arXiv:1805.10451 .
https://arxiv.org/abs/1805.10451
Xianfeng Gu, Feng Luo, Jian Sun, and Shing-Tung Yau. "Variational principles for minkowski type problems, discrete optimal transport", and discrete monge-ampere equations. Asian Journal of Mathematics (AJM), 20(2):383-398, 2016.
Na Lei,Kehua Su,Li Cui,Shing-Tung Yau,David Xianfeng Gu, "A Geometric View of Optimal Transportation and Generative Model", arXiv:1710.05488. https://arxiv.org/abs/1710.05488
Huidong L,Xianfeng Gu, Dimitris Samaras, "A Two-Step Computation of the Exact GAN Wasserstein Distance", ICML 2018.
声明:文章收集于网络,如有侵权,请联系小编及时处理,谢谢!
商业智能与数据分析群
兴趣范围包括各种让数据产生价值的办法,实际应用案例分享与讨论,分析工具,ETL工具,数据仓库,数据挖掘工具,报表系统等全方位知识
QQ群:81035754
文章版权归作者所有,未经允许请勿转载,若此文章存在违规行为,您可以联系管理员删除。
转载请注明本文地址:https://www.ucloud.cn/yun/4791.html
摘要:老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告,汇报了这方面的进展情况。深度学习的主要目的和功能之一就是从数据中学习隐藏的流形结构和流形上的概率分布。 (最近,哈佛大学丘成桐先生领导的团队,大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告,汇报了这方面的进展情况。这里是报告的简要记录,具体内容见【1...
摘要:最近老顾收到很多读者来信,绝大多数询问对抗生成网络的最优传输解释,以及和蒙日安培方程的关系。蒙日安培方程的几何解法硬件友好,可以用目前的并行实现。蒙日安培方程的正则性理论更加复杂,但是对于模式塌缩的理解非常关键。 最近老顾收到很多读者来信,绝大多数询问对抗生成网络的最优传输解释,以及和蒙日-安培方程的关系。很多问题涉及到经典蒙日-安培方程理论,这里我们从偏微分方程和几何角度介绍一下蒙日-安培...
摘要:老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告,汇报了这方面的进展情况。特别是深度学习网络的学习能力取决于网络的超参数,如何设计超参数,目前主要依赖于经验。 (最近,哈佛大学丘成桐先生领导的团队,大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为深度学习的几何观点的报告,汇报了这方面的进展情况。这里是报告的简要记录,具体内容...
摘要:我们将这些现象笼统称为广义的模式崩溃问题。这给出了模式崩溃的直接解释。而传统深度神经网络只能逼近连续映射,这一矛盾造成了模式崩溃。 春节前夕,北美遭遇极端天气,在酷寒中笔者来到哈佛大学探望丘成桐先生。新春佳节,本是普天同庆的日子,但对于孤悬海外的游子而言,却是更为凄凉难耐。远离父母亲朋,远离故国家园,自然环境寒风凛冽,飞雪漫天,社会环境疏离淡漠,冷清寂寥。在波士顿见到导师和朋友,倍感欣慰。笔...
阅读 4041·2021-11-22 13:53
阅读 1742·2021-09-23 11:52
阅读 2458·2021-09-06 15:02
阅读 990·2019-08-30 15:54
阅读 917·2019-08-30 14:15
阅读 2400·2019-08-29 18:39
阅读 677·2019-08-29 16:07
阅读 440·2019-08-29 13:13