【一文读懂Hinton最新Capsules论文】CNN 未来向何处去

摘要：未来向何处去做领袖不容易，要不断地指明方向。又譬如想识别在这些黑白图像中，是否包含从到的手写体数字，那么深度学习的传统做法是，输出一个维向量，，其中每个元素的取值范围是，表示出现相应数字的概率。老爷子的论文中，输出的是十个维向量，其中。

CNN 未来向何处去？

做领袖不容易，要不断地指明方向。所谓正确的方向，不仅前途要辉煌，而且道路要尽可能顺畅。

Geoffrey Hinton 是深度学习领域的领袖。2011 年，正当 CNN 模型爆发性地取得一个又一个靓丽成就时，老爷子却开始冷静地剖析 CNN 模型存在的致命弱点，指出前进的方向。

老爷子上周刚刚发表了一篇论文，题为 Dynamic Routing Between Capsules。一看这题目就预料得到，这篇论文一定会引起广泛关注。因为这题目里，涉及到两个概念，Capsule 和 Dynamic Routing。而这两个概念，正是老爷子主张的 CNN 前进的方向。

老爷子的论文，读起来略感晦涩，其实道理并不难懂。笔者尝试用浅显的语言，把论文梳理一下，或许有助于理解。

Capsule：实体的视觉数学表征

深度学习，其实就是一系列的张量变换。

从图像、视频、音频、文字等等原始数据中，通过一系列张量变换，筛选出特征数据，以便完成识别、分解、翻译等等任务。

譬如原始数据是 28 x 28 的黑白图像，每个黑白像素可以用 8 个 bits 来表达，那么这张黑白图像就可以用 28 * 28 * 8 的张量来表达，张量中每个元素的取值是布尔值，0 或者 1。

又譬如想识别在这些黑白图像中，是否包含从 0 到 9 的手写体数字，那么深度学习的传统做法是，输出一个 10 维向量，( x_{0}, x_{1}, ... x_{9} )，其中每个元素 x_{i} 的取值范围是 [0, 1.0]，表示出现相应数字的概率。

例如，输出的向量是 ( 0.2, 0.1, 0.7, 0.9, 0.2, ..., 0.1 )，那么意味着，图像中出现数字 2 的概率是 70%，出现数字 3 的概率是 90% 等等。

Capsule 的创新，在于改变了输出，不是输出一个向量，而是输出 10 个向量。每个向量分别表达某个数字的若干个属性。

老爷子的论文中，输出的是十个 16 维向量，( x_{i, j} ) 其中 i = 0 ... 15, j = 0, ... 9。也就是说，老爷子认为每个手写体数字包含 16 个属性，包含几个圆圈，几个弯勾，几个折角，几根横竖，弯勾折角的大小，笔划的粗细，整个字体的倾斜度，等等。

Capsule 的想法，不难理解。但是仔细想想，存在以下几个问题。

传统的图像识别的解决方案，是把识别问题转化为分类问题。这个方法已经足以解决识别问题。实体的视觉数学表征 capsule 的意义是什么？

如何证明 16 维的 capsule 向量，能够作为手写体数字的视觉数学表征？为什么不是 32 维或者更多？

Capsule 向量中的元素 x_{i}，与实体的属性之间的关联，是机器自动学习出来的。但是是否可以被人为预先强制指定？

低级 capsule 与高级 capsule 之间的关联关系，是机器自动学习出来的，还是可以被人为预先强制指定？

Capsule 的意义

老爷子试图用 capsule 向量，囊括实体的所有重要属性。如果某个实体的所有属性，都在图像中出现，那么可以确认，这个图像一定包含这个实体。所以他把这个向量，称为实体胶囊 capsule。

一个手写体数字，不管字体是否端正，笔划是粗还是细，圆圈和弯勾是大还是小，都用同一个胶囊 capsule 来表征。

一个轮胎，不管拍摄的角度如何，不管是正圆还是椭圆，不管轮毂是什么式样，也都可以用同一个胶囊 capsule 来表征。

说得抽象一点，capsule 就是实体的视觉的数学表征。

想起了词向量，word vector，词向量是文字词汇的数学表征。

能否把 capsule 和 word vector 统一起来，不管实体的表达是图像还是文字，都可以用同一个数学向量来表征？

论文中没有明说，但是老爷子多半心怀这个想法。

说得更直白一点，capsule 作为视觉数学表征，很可能是为了把视觉，听觉、阅读的原本相互独立的数学向量，统一起来，完成多模态机器学习的终极目标。

重构图像：验证 Capsule 的猜想 

假设 capsule 包含了某个实体的所有重要视觉属性，那么理论上来说，应该可以从 capsule 还原包含该实体的图像。

为了证明这个猜测，论文使用了一个神经网络，把 capsule 向量作为输入，重构手写体数字图像并输出。

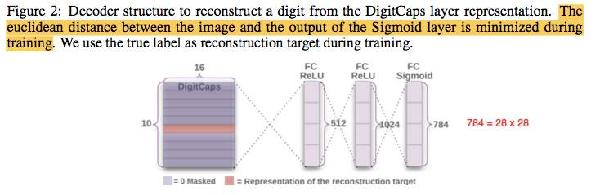
实验结果证明，capsule 确实能够重构出正确的手写体数字图像。

而且更让人惊奇的是，这些 capsules 中的某些属性，也就是 ( x_{i, j} ), i = 0...15，j = 0...9，其中的几个 x{i}，具有明确的物理意义，譬如手写体字体大小宽窄倾斜度，以及字体中弯勾圆弧等局部特征的大小位置等等。

为什么每个手写体数字只包含 16 个属性，而不是 32 个或者更多属性？

16 个属性，已经足以正确地重构手写体数字图像。32 个或者更多属性，无非是表达方式更细腻而已，这个问题不太重要。

Dynamic Routing：从原始数据中寻找实体属性的存在证据

Capsule 向量的元素 x_{i}，与实体的属性之间的关联，是人为确定的，还是机器自动对应的？

根据论文的描述，关联关系是机器自动对应的，所以在 capsule 向量 ( x_{i} ), i = 0...15 中，某些 x_{i} 的物理意义比较明确，其它 x_{i} 的物理意义却可能难以解释。

假如人为强制指定 capsule 中各个 x_{i}  的物理意义，换句话说，人为强制指定 capsule 向量元素 x_{i} 与实体属性之间的关联关系，是否会有助于提高识别精度，降低训练数据的数量？

回答这个问题之前，需要先了解的 capsule 向量中 ( x_{i} ) 的取值，是怎么来的。

前文说到，深度学习其实就是一系列的张量变换。通过一系列张量变换，从图像、视频、音频、文字等等原始数据中，筛选出特征数据，以便完成识别、分解、翻译等等任务。

论文使用了两层卷积神经网络，对原始黑白照片，也就是 28 * 28 * 8 的原始张量，用两层卷积，完成一系列张量变换，转变成新的张量 ( x_{attr, lon, lat, channel} ) ，attr  = 0 ... 7, lon = 0 ... 5, lat = 0 ... 5, channel = 0 ... 31。

这个新张量中的 ( x_{attr} ) 是初级 capsule，表达原始图像中值得注意的特征。其中 attr 代表初级 capsule 的属性，维度为 8。

新张量中的 ( x_{lon, lat} )  表示 capsule ( x_{attr} ) 在原始图像中的方位。经过张量变换后，28 * 28 的原始图像，被缩略为 6 * 6 个方位。( x_{channel} ) 是频道，类似于多机位拍摄同一个场景，全面表达 capsule 在原始图像中的视觉特点，总共有 32 个频道。

在新张量中，总共有 lon * lat * channel = 6 * 6 * 32 = 1152 个初级 capsule ( x_{attr} ) 。换句话说，经过一系列张量变换，从原始图像中，筛选出了 1152 个值得注意的图像特征。

高级 capsule 是前文说的十个手写体数字的 16 维属性向量，即 ( x_{attr, class} ), attr = 0 ... 15, class = 0 ... 9。

想识别原始图像中，是否包含手写体数字 3，也就是 class = 2，只需要把 1152 个初级 capsules，逐一与高级 capsule 向量 x_{*, 2}  做比对。

如何做比对呢？先做一次线性变换，把 8 维的初级 capsule，变换成 16 维的初级 capsule。然后计算 16 维的初级 capsule 与 16 维的高级 capsule 之间的余弦距离，也就是两个向量之间的点乘。

从每个高级 capsule 出发，在低级 capsules 中寻找它存在的证据，这个过程，就是 Dynamic Routing。

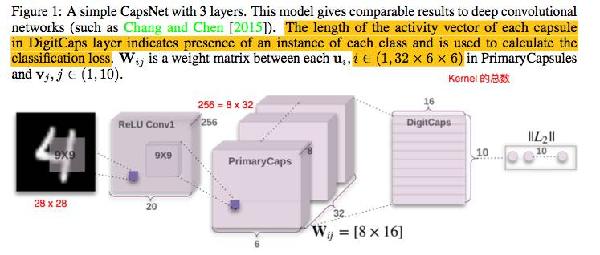
如果某一个高级 capsule 中每一个属性，都能在 1152 个初级 capsules 中，找到 “对应的” 一个或多个 capsules，那么就证实了高级 capsule 中的这个属性，确实在图像中存在。

如果某一个高级 capsule 中的全部 16 个属性，都能在 1152 个初级 capsules 中，找到存在的证据，那么就认定这个高级 capsule 在原始图像中存在。

如果有多个高级 capsules，都能在 1152 个初级 capsules 中，找到各自存在的证据，那么就认定在原始图像中存在多个高级 capsules。

Capsule 与先验知识

回到前文的问题，假如人为强制指定 capsule 中各个 x_{i}  的物理意义，换句话说，人为强制指定 capsule 向量元素 x_{i} 与实体属性之间的关联关系，是否会有助于提高识别精度，降低训练数据的数量？

假如人为强制指定 capsule 中某个 x_{i} 用于表达图像中是否存在圆圈，那么需要改变训练数据。

现在的训练数据，由输入和输出一对数据构成。输入数据是原始照片，输出数据是标签，说明原始照片中含有哪些数字。

如果要人为指定手写体数字的 capsule 中的元素 x_{i}，那么需要改变训练数据。譬如输入是原始照片，输出的标签，是说明这张照片中是否有圆圈。

改变训练数据有什么意义？一个可能的意义是 transfer learning。

一张轮胎的照片中，也包含圆圈。用现在的方法，轮胎的照片无助于手写体数字的识别，但是用  transfer learning，可以用轮胎的照片，来训练机器识别圆圈，然后把识别圆圈的算法模块，融合到手写体数字的识别系统中。

至于用这种方法，是否能够提高识别精度，降低训练数据的数量，需要做实验来验证。

Parse Tree：实体特征的多层次分解，及与先验知识的融合

在原始图像中，识别手写体数字，这个实验比较简单。

假如设计一个难度更高的实验，在原始图像中，识别自行车。自行车由两个轮胎，两个脚踏板，一个龙头和骨架等等构件组成。

要完成这个实验，需要先识别原始图像中，是否存在轮胎、脚踏板、龙头和骨架等等构件。然后识别这些构件之间的位置关系。

老爷子提议，用 Parse Tree 来分解整个识别任务，从原始图像，到图像特征，到不同构件，到自行车的识别。

Parse Tree 的生成，当然可以完全靠机器，从大量训练数据中自动学习。而且是一气呵成地完成各个环节，从原始图像，到图像特征，到不同构件，到最终的自行车识别。

但是如果融合先验知识，人为预先指定 Parse Tree 的结构，或许有助于把识别自行车的问题，拆解为若干子问题，分别识别轮胎、脚踏板、龙头和骨架等等构件，然后再把子模块整合成为自行车的识别系统。

当然，把大问题拆解为若干子问题，需要针对各个子问题，准备各自的训练数据。

这样做是否有利于提高识别精度，降低训练数据的数量，也需要做实验来验证。

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754