「自归一化神经网络」提出新型激活函数SELU

摘要：循环神经网络令语音和自然语言处理达到了新阶段。自归一化神经网络对于扰动是具有鲁棒性的，它在训练误差上并没有高方差见图。构建自归一化神经网络我们通过调整函数的属性以构建自归一化神经网络。

近日，arXiv 上公开的一篇 NIPS 投稿论文《Self-Normalizing Neural Networks》引起了圈内极大的关注，它提出了缩放指数型线性单元（SELU）而引进了自归一化属性，该单元主要使用一个函数 g 映射前后两层神经网络的均值和方差以达到归一化的效果。该论文的作者为 Sepp Hochreiter，也就是当年和 Jürgen Schmidhuber 一起发明 LSTM 的大牛，之前的 ELU 同样来自于他们组。有趣的是，这篇 NIPS 投稿论文虽然只有 9 页正文，却有着如同下图一样的 93 页证明附录。

在这篇文章中，机器之心对该论文进行了概要介绍。此外，Github 上已有人做出了论文中提出的 SELUs 与 ReLU 和 Leaky ReLU 的对比，我们也对此对比进行了介绍。

论文地址：https://arxiv.org/pdf/1706.02515.pdf

摘要：深度学习不仅通过卷积神经网络（CNN）变革了计算机视觉，同时还通过循环神经网络（RNN）变革了自然语言处理。然而，带有标准前馈神经网络（FNN）的深度学习很少有成功的案例。通常表现良好的 FNN 都只是浅层模型，因此不能挖掘多层的抽象表征。所以我们希望引入自归一化神经网络（self-normalizing neural networks/SNNs）以帮助挖掘高层次的抽象表征。虽然批归一化要求较精确的归一化，但 SNN 的神经元激励值可以自动地收敛到零均值和单位方差。SNN 的激活函数即称之为「可缩放指数型线性单元（scaled exponential linear units/SELUs）」，该单元引入了自归一化的属性。使用 Banach 的不动点定理（fixed-point theorem），我们证明了激励值逼近于零均值和单位方差并且通过许多层的前向传播还是将收敛到零均值和单位方差，即使是存在噪声和扰动的情况下也是这样。这种 SNN 收敛属性就允许 (1) 训练许多层的深度神经网络，同时 (2) 采用强正则化、(3) 令学习更具鲁棒性。此外，对于不逼近单位方差的激励值，我们证明了其方差存在上确界和下确界，因此梯度消失和梯度爆炸是不可能出现的。同时我们采取了 (a) 来自 UCI 机器学习库的 121 个任务，并比较了其在 (b) 新药发现基准和 (c) 天文学任务上采用标准 FNN 和其他机器学习方法（如随机森林、支持向量机等）的性能。SNN 在 121 个 UCI 任务上显著地优于所有竞争的 FNN 方法，并在 Tox21 数据集上超过了所有的竞争方法，同时 SNN 还在天文数据集上达到了新纪录。该实现的 SNN 架构通常比较深，实现可以在以下链接获得：http://github.com/bioinf-jku/SNNs。

前言

深度学习在许多不同的基准上都达到了新记录，并促进了各种商业应用的发展 [25, 33]。循环神经网络（RNN）[18] 令语音和自然语言处理达到了新阶段。而与其相对应的卷积神经网络（CNN）[24] 则变革了计算机视觉和视频任务。

然而，当我们回顾 Kaggle 竞赛时，通常很少有任务是和计算机视觉或序列任务相关的，梯度提升、随机森林或支持向量机（SVM）通常在绝大多数任务上都能取得十分优秀的表现。相反，深度学习却表现并不优异。

为了更鲁棒地训练深度卷积神经网络（CNN），批归一化发展成了归一化神经元激励值为 0 均值和单位方差 [20] 的标准方法。层级归一化（Layer normalization）[2] 确保了 0 均值和单位方差，因为如果上一层的激励值有 0 均值和单位方差，那么权值归一化 [32] 就确保了 0 均值和单位方差。然而，归一化技术在训练时通常会受到随机梯度下降（SGD）、随机正则化（如 dropout）和估计归一化参数所扰动。

自归一化神经网络（SNN）对于扰动是具有鲁棒性的，它在训练误差上并没有高方差（见图 1）。SNN 令神经元激励值达到 0 均值和单位方差，从而达到和批归一化相类似的效果，而这种归一化效果可以在许多层级的训练中都保持鲁棒性。SNN 基于缩放指数型线性单元（SELU）而引进了自归一化属性，因此方差稳定化（variance stabilization）也就避免了梯度爆炸和梯度消失。

自归一化神经网络（SNN）

归一化和 SNN

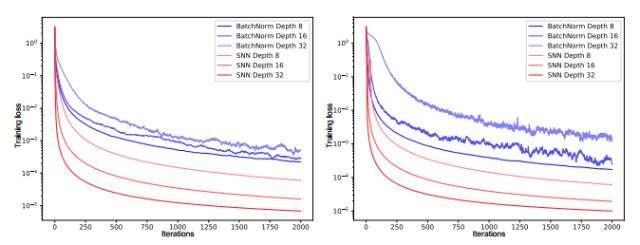
图 1：左边图表和右边图表的 y 轴展示了带有批归一化（BatchNorm）和自归一化（SNN）的前馈神经网络（FNN）的训练损失，x 轴代表迭代次数，该训练在 MNIST 数据集和 CIFAR10 数据集上完成。我们测试的神经网络有 8、16 和 32 层，且学习率为 1e-5。采用批归一化的 FNN 由于扰动出现了较大的方差，但 SNN 并不会出现较大的方差，因此 SNN 对扰动会更加鲁棒，同时学习的速度也会更加迅速。

构建自归一化神经网络

我们通过调整函数 g 的属性以构建自归一化神经网络。函数 g 只有两个可设计的选择：(1) 激活函数和 (2) 权重的初始化。

通过映射函数 g 派生均值和方差

我们假设 xi 之间相互独立，并且有相同的均值μ 和方差 ν，当然独立性假设通常得不到满足。我们将在后面详细描述独立性假设。函数 g 将前一层神经网络激励值的均值和方差映射到下一层中激励值 y 的均值μ˜ = E(y) 和方差ν˜ = Var(y) 中：

这些积分的解析解可以通过以下方程求出：

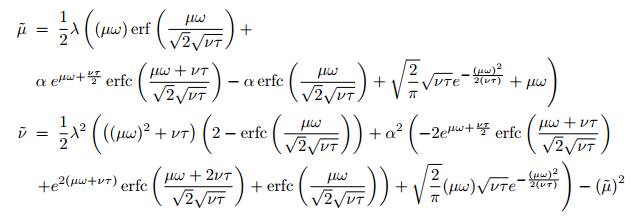
归一化权值的稳定和诱集不动点（Attracting Fixed Point）（0，1）

非归一化权值的稳定和诱集不动点（Attracting Fixed Point）

在学习中归一化的权值向量 w 并得不到保证。

图 2：对于ω = 0 和 τ = 1，上图描述了将均值μ（x 轴）和方差 v（y 轴）映射到下一层的均值 μ˜和方差ν˜。箭头展示了由 g : (μ, ν) → (˜μ, ν˜) 映射的 (μ, ν) 的方向。映射 g 的不动点为 (0, 1)。

定理一（稳定和诱集不动点）

该章节给出了定理证明的概要（附录 Section A3 给出详细的证明）。根据 Banach 不动点定理（fixed point theorem），我们证明了存在的诱集和稳定不动点。

定理二（降低 v）

该定理的详细证明可以在附录 Section A3 中找到。因此，当映射经过许多层级时，在区间 [3, 16] 内的方差被映射到一个小于 3 的值。

定理三（提高 v）

该定理的证明可以在附录 Section A3 找到。所有映射 g(Eq. (3)) 的不动点 (μ, ν) 确保了 0.8 =< τ时ν ˜ >0.16，0.9 =< τ时ν ˜> 0.24。

初始化

因为 SNN 有归一化权值的 0 均值和单位方差不动点，所以我们初始化 SNN 来满足一些期望的约束条件。

新的 Dropout 技术

标准的 Dropout 随机地设定一个激励值 x 以 1-q 的概率等于 0，其中 0 < q < 1。为了保持均值，激励值在训练中通过 1/q 进行缩放。

中心极限定理和独立性假设的适用性

实验（略）

结论

我们提出了自归一化神经网络，并且已经证明了当神经元激励在网络中传播时是在朝零均值（zero mean）和单位方差（unit variance）的趋势发展的。而且，对于没有接近单位方差的激励，我们也证明了方差映射的上线和下限。于是 SNN 不会产梯度消失和梯度爆炸的问题。因此，SNN 非常适用于多层的结构，这使我们可以引入一个全新的正则化（regularization）机制，从而更稳健地进行学习。在 121UCI 基准数据集中，SNN 已经超过了其他一些包括或不包括归一化方法的 FNN，比如批归一化（batch）、层级归一化（layer）、权值归一化（weight normalization）或其它特殊结构（Highway network 或 Residual network）。SNN 也在药物研发和天文学任务中产生了完美的结果。和其他的 FNN 网络相比，高性能的 SNN 结构通常深度更深。

附录（略）

SELU 与 Relu、Leaky Relu 的对比

昨日，Shao-Hua Sun 在 Github 上放出了 SELU 与 Relu、Leaky Relu 的对比，机器之心对比较结果进行了翻译介绍，具体的实现过程可参看以下项目地址。

项目地址：https://github.com/shaohua0116/Activation-Visualization-Histogram

描述

本实验包括《自归一化神经网络》（Self-Normalizing Neural Networks）这篇论文提出的 SELUs（缩放指数型线性单元）的 Tensorflow 实现。也旨在对 SELUs，ReLU 和 Leaky-ReLU 等进行对比。本实验的重点是在 Tensorboard 上对激励进行可视化。

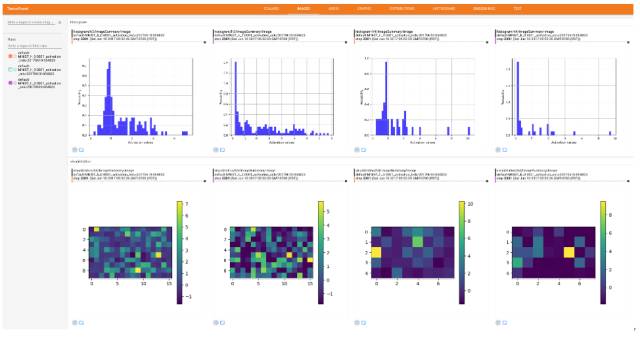
SELUs（缩放指数型线性单元），ReLU 和 Leaky-ReLU 的可视化和直方图对比

理论上，我们希望每一层的激励的均值为 0（zero mean），方差为 1（unit variance），来使在各层之间传播的张量收敛（均值为 0，方差为 1）。这样一来就避免了梯度突然消失或爆炸性增长的问题，从而使学习过程更加稳定。在本实验中，作者提出 SELUs（缩放指数型线性单元），旨在对神经元激励进行自动地转移（shift）和重缩放 (rescale)，在没有明确的归一化的情况下去实现零均值和单位方差。

为了用实验证明所提出的激励的有效性，一个包含三个卷积层的卷积神经网络（也包括三个完全连接层——fully connected layers）在 MNIST, SVHN 和 CIFAR10 数据集上进行训练，来进行图像分类。为了克服 Tensorboard 显示内容的一些限制，我们引入了绘图库 Tensorflow Plot 来弥补 Python 绘图库和 Tensorboard 间的差距。以下是一些例子。

在 Tensorboard 上的激励值直方图

在 Tensorboard 上的激励值可视化

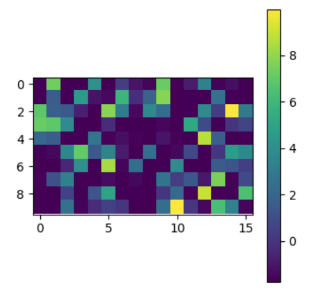
实现模型在三个公开的数据集上进行的训练与测试：MNIST、SVHN 和 CIFAR-10。

结果

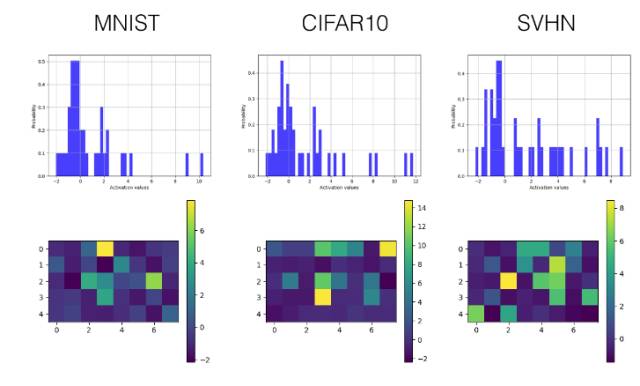
下面我们只选择性展示了最后一个卷积层（第三层）和较早的全连接层（第四层）的直方图和可视化激励值图。

SELU

卷积层

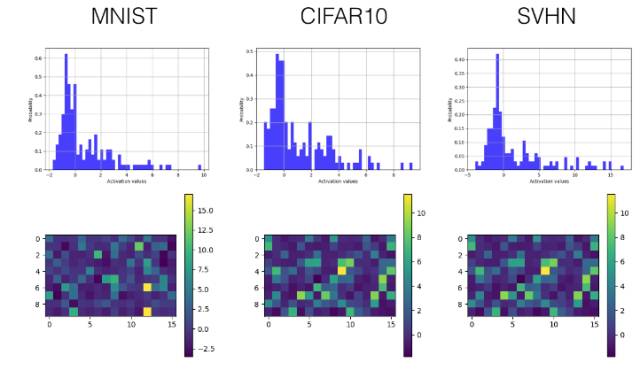
全连接层

ReLU

卷积层

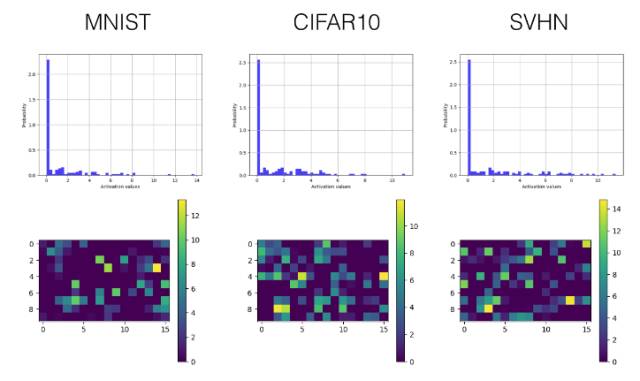
全连接层

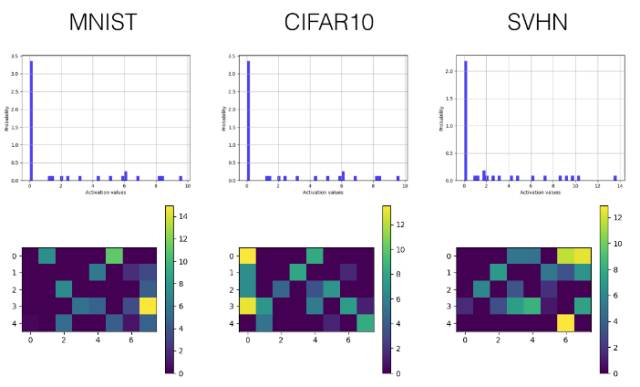
Leaky ReLU

卷积层

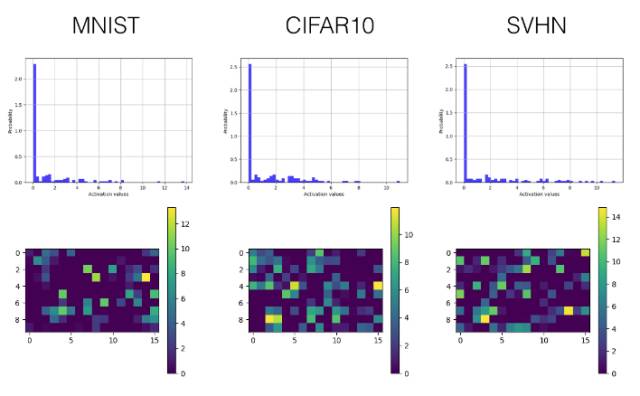
全连接层

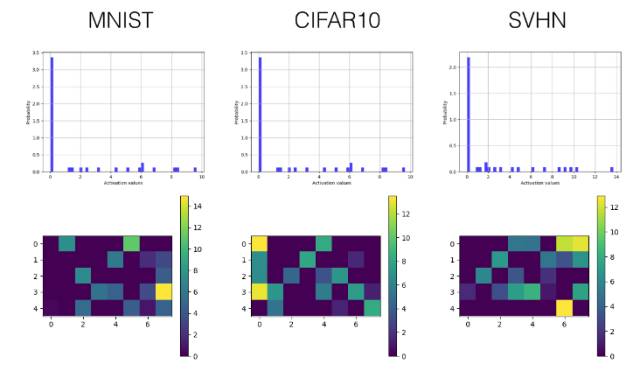
相关工作

Self-Normalizing Neural Networks by Klambauer et. al

Rectified Linear Units Improve Restricted Boltzmann Machines by Nair et. al.

Empirical Evaluation of Rectified Activations in Convolutional Network by Xu et. al.

作者

Shao-Hua Sun / @shaohua0116 (https://shaohua0116.github.io/)。

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754