资讯专栏INFORMATION COLUMN

摘要:什么是激活函数,它在神经网络模型中是如何使用的激活函数对于人工神经网络模型去学习理解非常复杂和非线性的函数来说具有十分重要的作用。线性函数一个一级多项式。
什么是人工神经网络?
现在,我相信我们大家都很熟悉什么是A-NN了,但接下来请允许我按照自己的理解给A-NN下个定义——它是一个强健有力的,同时也非常复杂的机器学习技术,它可以模仿人类的大脑,继而模仿大脑的运作。
正如我们的人脑一样,在一个层次上和神经元网络中有数百万个神经元,这些神经元通过一种称之为synapses(突触)的结构彼此紧紧相连。它可以通过 Axons(轴突),将电信号从一个层传递到另一个层。这就是我们人类学习事物的方式。 每当我们看到、听到、感觉和思考时,一个突触(电脉冲)从层次结构中的一个神经元被发射到另一个神经元,这使我们能够从我们出生的那一天起,就开始学习、记住和回忆我们日常生活中的东西。
好的,接下来我保证大家看到的不再是生物学领域的知识了。
什么是激活函数,它在神经网络模型中是如何使用的?
激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
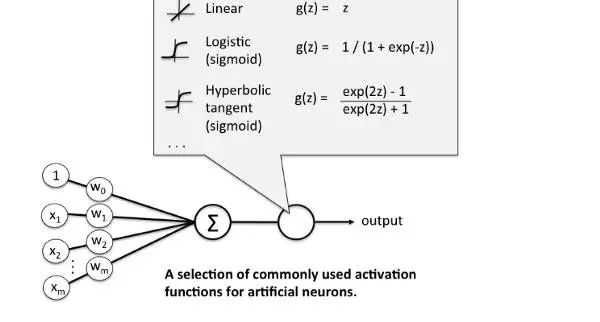
而在A-NN中的具体操作是这样的,我们做输入(X)和它们对应的权重(W)的乘积之和,并将激活函数f(x)应用于其获取该层的输出并将其作为输入馈送到下一个层。
问题是,为什么我们不能在不激活输入信号的情况下完成此操作呢?
如果我们不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。现如今,线性方程是很容易解决的,但是它们的复杂性有限,并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型(Linear regression Model)罢了,它功率有限,并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数,而且还要比这复杂得多。同样是因为没有激活函数,我们的神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术,诸如深度学习(Deep learning),来理解一些复杂的事情,一些相互之间具有很多隐藏层的非线性问题,而这也可以帮助我们了解复杂的数据。
那么为什么我们需要非线性函数?
非线性函数是那些一级以上的函数,而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型,以及可以将输入映射到输出的任意复杂函数。神经网络被认为是通用函数近似器(Universal Function Approximators)。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。
而这一切都归结于这一点,我们需要应用激活函数f(x),以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。因此,使用非线性激活函数,我们便能够从输入输出之间生成非线性映射。
激活函数的另一个重要特征是:它应该是可以区分的。我们需要这样做,以便在网络中向后推进以计算相对于权重的误差(丢失)梯度时执行反向优化策略,然后相应地使用梯度下降或任何其他优化技术优化权重以减少误差。
只要永远记住要做:
“输入时间权重,添加偏差和激活函数”
最流行的激活函数类型
1.Sigmoid函数或者Logistic函数
2.Tanh — Hyperbolic tangent(双曲正切函数)
3.ReLu -Rectified linear units(线性修正单元)
Sigmoid激活函数:它是一个f(x)= 1/1 + exp(-x)形式的激活函数。它的值区间在0和1之间,是一个S形曲线。它很容易理解和应用,但使其不受欢迎的主要原因是:
·梯度消失问题
·其次,它的输出不是以0为中心。它的梯度更新在不同的方向上且走得太远。 0
文章版权归作者所有,未经允许请勿转载,若此文章存在违规行为,您可以联系管理员删除。
转载请注明本文地址:https://www.ucloud.cn/yun/4552.html
摘要:可以参见以下相关阅读创造更多数据上一小节说到了有了更多数据,深度学习算法通常会变的更好。 导语我经常被问到诸如如何从深度学习模型中得到更好的效果的问题,类似的问题还有:我如何提升准确度如果我的神经网络模型性能不佳,我能够做什么?对于这些问题,我经常这样回答,我并不知道确切的答案,但是我有很多思路,接着我会列出了我所能想到的所有或许能够给性能带来提升的思路。为避免一次次罗列出这样一个简单的列表...
摘要:希望大家在这浮夸的前端圈里,保持冷静,坚持每天花分钟来学习与思考。 今天的React题没有太多的故事…… 半个月前出了248个Vue的知识点,受到很多朋友的关注,都强烈要求再出多些React相前的面试题,受到大家的邀请,我又找了20多个React的使用者,他们给出了328道React的面试题,由我整理好发给大家,同时发布在了前端面试每日3+1的React专题,希望对大家有所帮助,同时大...
摘要:前端面试每日题,以面试题来驱动学习,每天进步一点让努力成为一种习惯,让奋斗成为一种享受相信坚持的力量项目地址推荐欢迎跟一起折腾前端,系统整理前端知识,目前正在折腾,打算打通算法与数据结构的任督二脉。 《论语》,曾子曰:吾日三省吾身(我每天多次反省自己)。 前端面试每日3+1题,以面试题来驱动学习,每天进步一点! 让努力成为一种习惯,让奋斗成为一种享受!相信 坚持 的力量!!! 项目...
摘要:前端面试每日题,以面试题来驱动学习,每天进步一点让努力成为一种习惯,让奋斗成为一种享受相信坚持的力量项目地址推荐欢迎跟一起折腾前端,系统整理前端知识,目前正在折腾,打算打通算法与数据结构的任督二脉。 《论语》,曾子曰:吾日三省吾身(我每天多次反省自己)。 前端面试每日3+1题,以面试题来驱动学习,每天进步一点! 让努力成为一种习惯,让奋斗成为一种享受!相信 坚持 的力量!!! 项目...
摘要:注意,鼠标点击后不松开,此伪类一直激活,直到松开鼠标。哪些伪类会同时激活并影响显示效果第一,其实和两个伪类之间顺序无所谓。此时链接依然存在,只是已经被访问过,所以伪类不再激活。 博主的博客地址:Stillwater的个人博客转载请注明原文链接 一、标签常用的伪类概述 a:link{color:blue} ...
阅读 966·2021-11-24 09:38
阅读 1045·2021-11-23 09:51
阅读 3025·2021-11-16 11:44
阅读 1826·2021-09-22 15:52
阅读 1737·2021-09-10 11:20
阅读 1449·2019-08-30 13:47
阅读 1370·2019-08-29 12:36
阅读 3376·2019-08-26 10:43