令人拍案叫绝的Wasserstein GAN

摘要：测度是高维空间中长度面积体积概念的拓广，可以理解为超体积。前作其实已经针对第二点提出了一个解决方案，就是对生成样本和真实样本加噪声，直观上说，使得原本的两个低维流形弥散到整个高维空间，强行让它们产生不可忽略的重叠。

在GAN的相关研究如火如荼甚至可以说是泛滥的今天，一篇新鲜出炉的arXiv论文《Wasserstein GAN》却在Reddit的Machine Learning频道火了，连Goodfellow都在帖子里和大家热烈讨论，这篇论文究竟有什么了不得的地方呢？ 

要知道自从2014年Ian Goodfellow提出以来，GAN就存在着训练困难、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题。从那时起，很多论文都在尝试解决，但是效果不尽人意，比如最有名的一个改进DCGAN依靠的是对判别器和生成器的架构进行实验枚举，最终找到一组比较好的网络架构设置，但是实际上是治标不治本，没有彻底解决问题。而今天的主角Wasserstein GAN（下面简称WGAN）成功地做到了以下爆炸性的几点：

彻底解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度

基本解决了collapse mode的问题，确保了生成样本的多样性 

训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高（如题图所示）

以上一切好处不需要精心设计的网络架构，最简单的多层全连接网络就可以做到

那以上好处来自哪里？这就是令人拍案叫绝的部分了——实际上作者整整花了两篇论文，在第一篇《Towards Principled Methods for Training Generative Adversarial Networks》里面推了一堆公式定理，从理论上分析了原始GAN的问题所在，从而针对性地给出了改进要点；在这第二篇《Wasserstein GAN》里面，又再从这个改进点出发推了一堆公式定理，最终给出了改进的算法实现流程，而改进后相比原始GAN的算法实现流程却只改了四点：

判别器最后一层去掉sigmoid

生成器和判别器的loss不取log

每次更新判别器的参数之后把它们的值截断到不超过一个固定常数c

不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

算法截图如下：

改动是如此简单，效果却惊人地好，以至于Reddit上不少人在感叹：就这样？没有别的了？ 太简单了吧！这些反应让我想起了一个颇有年头的鸡汤段子，说是一个工程师在电机外壳上用粉笔划了一条线排除了故障，要价一万美元——画一条线，1美元；知道在哪画线，9999美元。上面这四点改进就是作者Martin Arjovsky划的简简单单四条线，对于工程实现便已足够，但是知道在哪划线，背后却是精巧的数学分析，而这也是本文想要整理的内容。

本文内容分为五个部分：

原始GAN究竟出了什么问题？（此部分较长）

WGAN之前的一个过渡解决方案 

Wasserstein距离的优越性质

从Wasserstein距离到WGAN

总结

理解原文的很多公式定理需要对测度论、 拓扑学等数学知识有所掌握，本文会从直观的角度对每一个重要公式进行解读，有时通过一些低维的例子帮助读者理解数学背后的思想，所以不免会失于严谨，如有引喻不当之处，欢迎在评论中指出。

以下简称《Wassertein GAN》为“WGAN本作”，简称《Towards Principled Methods for Training Generative Adversarial Networks》为“WGAN前作”。

WGAN源码实现：martinarjovsky/WassersteinGAN

第一部分：原始GAN究竟出了什么问题？

第一种原始GAN形式的问题

一句话概括：判别器越好，生成器梯度消失越严重。WGAN前作从两个角度进行了论证，第一个角度是从生成器的等价损失函数切入的。

首先从公式1可以得到，在生成器G固定参数时最优的判别器D应该是什么。对于一个具体的样本，它可能来自真实分布也可能来自生成分布，它对公式1损失函数的贡献是

然而GAN训练有一个trick，就是别把判别器训练得太好，否则在实验中生成器会完全学不动（loss降不下去），为了探究背后的原因，我们就可以看看在极端情况——判别器最优时，生成器的损失函数变成什么。给公式2加上一个不依赖于生成器的项，使之变成

流形（manifold）是高维空间中曲线、曲面概念的拓广，我们可以在低维上直观理解这个概念，比如我们说三维空间中的一个曲面是一个二维流形，因为它的本质维度（intrinsic dimension）只有2，一个点在这个二维流形上移动只有两个方向的自由度。同理，三维空间或者二维空间中的一条曲线都是一个一维流形。

测度（measure）是高维空间中长度、面积、体积概念的拓广，可以理解为“超体积”。

接着作者写了很多公式定理从第二个角度进行论证，但是背后的思想也可以直观地解释：

有了这些理论分析，原始GAN不稳定的原因就彻底清楚了：判别器训练得太好，生成器梯度消失，生成器loss降不下去；判别器训练得不好，生成器梯度不准，四处乱跑。只有判别器训练得不好不坏才行，但是这个火候又很难把握，甚至在同一轮训练的前后不同阶段这个火候都可能不一样，所以GAN才那么难训练。

实验辅证如下：

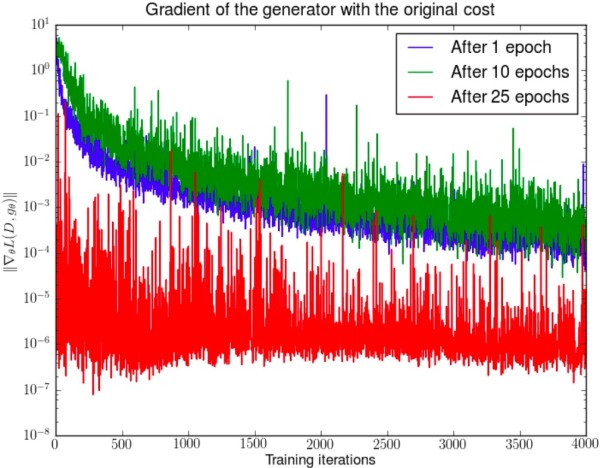
WGAN前作Figure 2。先分别将DCGAN训练1，20，25个epoch，然后固定生成器不动，判别器重新随机初始化从头开始训练，对于第一种形式的生成器loss产生的梯度可以打印出其尺度的变化曲线，可以看到随着判别器的训练，生成器的梯度均迅速衰减。注意y轴是对数坐标轴。

第二种原始GAN形式的问题

一句话概括：最小化第二种生成器loss函数，会等价于最小化一个不合理的距离衡量，导致两个问题，一是梯度不稳定，二是collapse mode即多样性不足。WGAN前作又是从两个角度进行了论证，下面只说第一个角度，因为对于第二个角度我难以找到一个直观的解释方式，感兴趣的读者还是去看论文吧（逃）。

第一部分小结：在原始GAN的（近似）最优判别器下，第一种生成器loss面临梯度消失问题，第二种生成器loss面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚不平衡导致mode collapse这几个问题。

实验辅证如下：

WGAN前作Figure 3。先分别将DCGAN训练1，20，25个epoch，然后固定生成器不动，判别器重新随机初始化从头开始训练，对于第二种形式的生成器loss产生的梯度可以打印出其尺度的变化曲线，可以看到随着判别器的训练，蓝色和绿色曲线中生成器的梯度迅速增长，说明梯度不稳定，红线对应的是DCGAN相对收敛的状态，梯度才比较稳定。

第二部分：WGAN之前的一个过渡解决方案 

原始GAN问题的根源可以归结为两点，一是等价优化的距离衡量（KL散度、JS散度）不合理，二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。

WGAN前作其实已经针对第二点提出了一个解决方案，就是对生成样本和真实样本加噪声，直观上说，使得原本的两个低维流形“弥散”到整个高维空间，强行让它们产生不可忽略的重叠。而一旦存在重叠，JS散度就能真正发挥作用，此时如果两个分布越靠近，它们“弥散”出来的部分重叠得越多，JS散度也会越小而不会一直是一个常数，于是（在第一种原始GAN形式下）梯度消失的问题就解决了。在训练过程中，我们可以对所加的噪声进行退火（annealing），慢慢减小其方差，到后面两个低维流形“本体”都已经有重叠时，就算把噪声完全拿掉，JS散度也能照样发挥作用，继续产生有意义的梯度把两个低维流形拉近，直到它们接近完全重合。以上是对原文的直观解释。

在这个解决方案下我们可以放心地把判别器训练到接近最优，不必担心梯度消失的问题。而当判别器最优时，对公式9取反可得判别器的最小loss为

第三部分：Wasserstein距离的优越性质

第四部分：从Wasserstein距离到WGAN

既然Wasserstein距离有如此优越的性质，如果我们能够把它定义为生成器的loss，不就可以产生有意义的梯度来更新生成器，使得生成分布被拉向真实分布吗？

上文说过，WGAN与原始GAN第一种形式相比，只改了四点：

判别器最后一层去掉sigmoid

生成器和判别器的loss不取log

每次更新判别器的参数之后把它们的值截断到不超过一个固定常数c

不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

前三点都是从理论分析中得到的，已经介绍完毕；第四点却是作者从实验中发现的，属于trick，相对比较“玄”。作者发现如果使用Adam，判别器的loss有时候会崩掉，当它崩掉时，Adam给出的更新方向与梯度方向夹角的cos值就变成负数，更新方向与梯度方向南辕北辙，这意味着判别器的loss梯度是不稳定的，所以不适合用Adam这类基于动量的优化算法。作者改用RMSProp之后，问题就解决了，因为RMSProp适合梯度不稳定的情况。

对WGAN作者做了不少实验验证，本文只提比较重要的三点。第一，判别器所近似的Wasserstein距离与生成器的生成图片质量高度相关，如下所示（此即题图）：

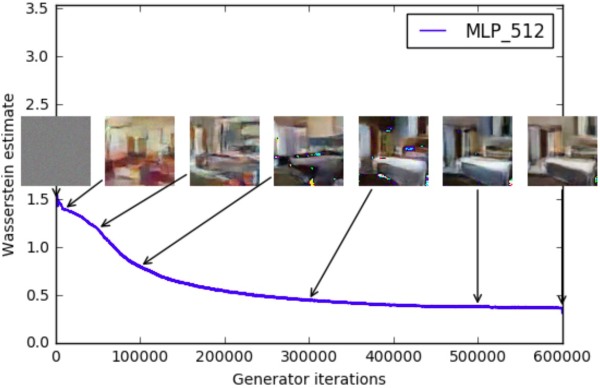
最后补充一点论文没提到，但是我个人觉得比较微妙的问题。判别器所近似的Wasserstein距离能够用来指示单次训练中的训练进程，这个没错；接着作者又说它可以用于比较多次训练进程，指引调参，我倒是觉得需要小心些。比如说我下次训练时改了判别器的层数、节点数等超参，判别器的拟合能力就必然有所波动，再比如说我下次训练时改了生成器两次迭代之间，判别器的迭代次数，这两种常见的变动都会使得Wasserstein距离的拟合误差就与上次不一样。那么这个拟合误差的变动究竟有多大，或者说不同的人做实验时判别器的拟合能力或迭代次数相差实在太大，那它们之间还能不能直接比较上述指标，我都是存疑的。

第五部分：总结

WGAN前作分析了Ian Goodfellow提出的原始GAN两种形式各自的问题，第一种形式等价在最优判别器下等价于最小化生成分布与真实分布之间的JS散度，由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性，使得生成器面临梯度消失的问题；第二种形式在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度，又要较大化其JS散度，相互矛盾，导致梯度不稳定，而且KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性，导致collapse mode现象。

WGAN前作针对分布重叠问题提出了一个过渡解决方案，通过对生成样本和真实样本加噪声使得两个分布产生重叠，理论上可以解决训练不稳定的问题，可以放心训练判别器到接近最优，但是未能提供一个指示训练进程的可靠指标，也未做实验验证。

WGAN本作引入了Wasserstein距离，由于它相对KL散度与JS散度具有优越的平滑特性，理论上可以解决梯度消失问题。接着通过数学变换将Wasserstein距离写成可求解的形式，利用一个参数数值范围受限的判别器神经网络来较大化这个形式，就可以近似Wasserstein距离。在此近似最优判别器下优化生成器使得Wasserstein距离缩小，就能有效拉近生成分布与真实分布。WGAN既解决了训练不稳定的问题，也提供了一个可靠的训练进程指标，而且该指标确实与生成样本的质量高度相关。作者对WGAN进行了实验验证。

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754