深度学习这么讲你肯定能读懂

摘要：梯度下降算法梯度是个啥我想最开始接触梯度的各位是在方向导数那一章接触这一概念的，如果老师没怎么讲的话可能有些人还不知道梯度是个向量。在二维条件下，因为有了两个偏导数，所以这个向量能表示一圈。

讲你肯定能懂的机器学习多维极值求解

事先说明

本文面向学习过高等数学统计学和线性代数基础知识的本科生，并假设读者拥有基本的矩阵运算和求导运算的相关知识，类似梯度，方向导数、Hessian Matrix这些东西不懂也没关系，我会用尽可能通俗的语言说明运算中的意义。

那么从最简单的开始。

梯度下降算法

梯度是个啥?我想最开始接触梯度的各位是在方向导数那一章接触这一概念的，如果老师没怎么讲的话可能有些人还不知道梯度是个向量。当你学梯度的时候，所有的概念全都是在二元函数下的，well，也写想象力不是很丰富的同学可能不知道这是个啥。来，我们降维先。

多维条件下是曲面对函数的一阶偏导数向量，那么在一维条件下梯度会是什么的?显然就木有偏导数了，只有一个东西，当然你也可以把它写成向量的形式，就是一个导数，只不过现在变成一维的了，所以方向只有俩，向左和向右。值为正的时候向右，值为负的时候向左，值大值小不影响方向只影响距离。

在二维条件下，因为有了两个偏导数，所以这个向量能表示一圈。如果你以前看过些文章或者视频或者什么ppt之类的东西，大概你会听说一种说法：“梯度是曲面中最陡峭的方向，这个方向是下降最快的方向。”实际上这种说法是不准确的，从一维的角度来看，“梯度”其实是上升最快的方向，比如

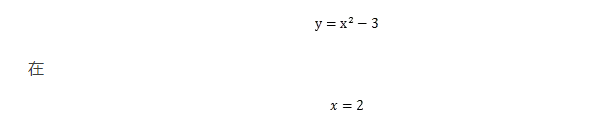
处的导数是1，方向向右，这个方向函数是增长的。同样二维也是如此。只不过大部分迭代公式中在梯度的前面会加一个负号，比如这个

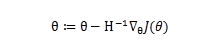
。所以也就直接认为它代表了下降最快的方向了。

直观上，你可以理解为，梯度就是一个和曲面等高线垂直的法线，冲着增高的那边。就像下图：

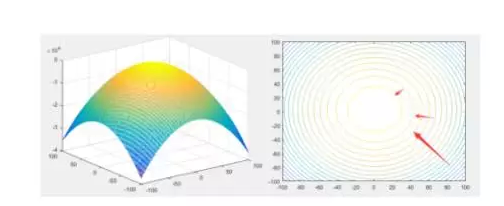
那么它相反的方向就是下降的方向啦，函数的极值点导数都是0的，也就是说，你沿着梯度方向一直走，如果最终收敛到一个点，那肯定就是一个极值点，如果不收敛，说明可能不存在极值点哈(这里因为有步长的涉及，在求解的时候会遇到明明有极值点却没有收敛的问题，后面会提到)。

举个例子，在一维下用梯度下降算法求解极值点的问题。这里我先举一个方便验算的例子，方便大家理解。

，这里 就是步长，用来调节每一次移动的距离，你也可能听过一些 不能过大也不能过小的看起来只能靠经验的废话。如果你是刚刚入门，可能写点程序，然后不断试，但是实际上 较优的也是可以算的，只不过那又是另一门带有好多论文的学科了。

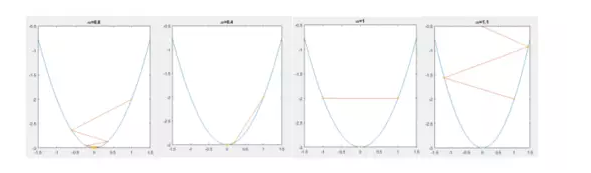
不同的 得到不一样的迭代效果，收敛或者震荡收敛，周期震荡或者直接发散，但是有的时候，算一遍

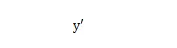
很费劲啊!这里例子简单，要是碰到TB级的数据那真的是要死了。这还能去试?这里简单的说一下怎么设置 ，首先你要确定x是收敛的。所以公式

实际上如果 控制在0到1/2之间会收敛更快，因为震荡收敛总会造成一些重复计算。

二维上的梯度下降能干啥呢?

还是举一个简单的例子，这里直接连数据都是最简单的。你有两个点(4,4),(6,5)，你想画一条线使得线和两个点之间的距离平方和最小，当然你也可以口算出来，但是我们依然是为了看一下作用，直接写公式对于一些人来说真的会蒙。

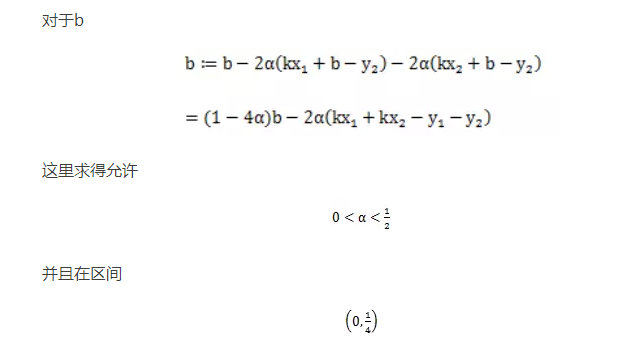
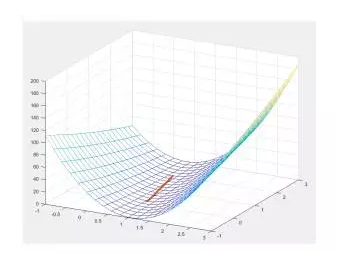
内不会震荡，梯度计算方向在二维曲面震荡起来长啥样啊。来来来画个图。开始震荡的部分我想我得给他个特写。

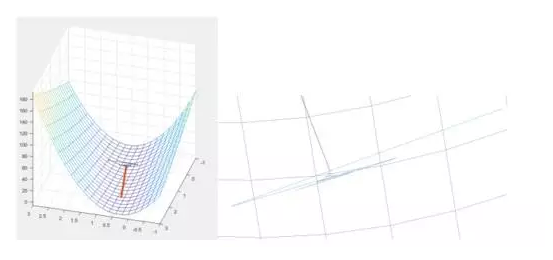
不过瘾?来看这个

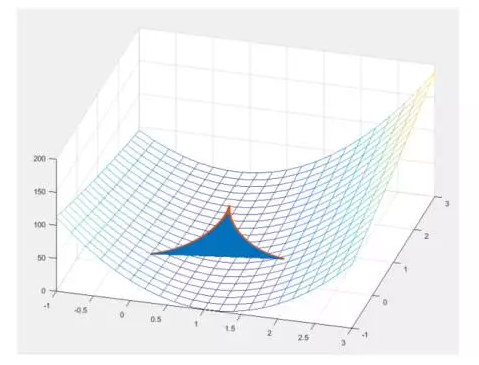
大致知道啥意思就行了哈。

在不震荡的情况下就显得特别简洁了。一条线走回去。

当然教科书上数学书上肯定不会这么写例子，为了公式的简洁，最后改为:

了, 则表示所有参数的集合。咦?公式多了个1/2是哪来的?在这里实际上这个值是多少都无所谓，因为两个偏导数都带着这个1/2不影响梯度方向，只影响步长，而步长又可以由调节，我们可以理解为，加了它，导数写起来好看^_^。就像下面这样。

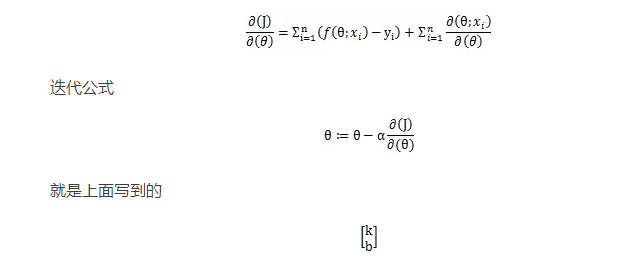
一个列向量。

更多维的原理都一样，梯度下降就讲到这。

牛顿法

提到牛顿法的时候，你可能在小的时候听说过，一个用来迭代求零点的方法，稍微提一下。

，然后不断的试值，唔~~还是来画图吧。

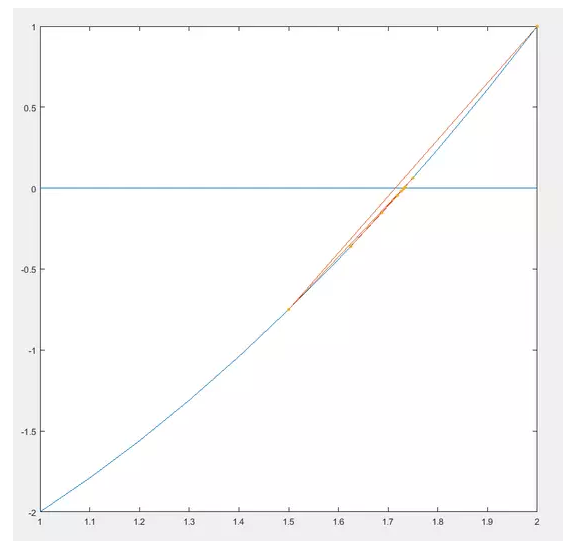
你也可以看到他们的迭代过程，当然这个不叫牛顿法，这个叫二分法，比较low哈，看到没，震荡了，震荡收敛慢。

当趋近于0的时候他俩才近似。而牛顿法就是用切线来快速逼近零点的，不会震荡呦，画图吧先。

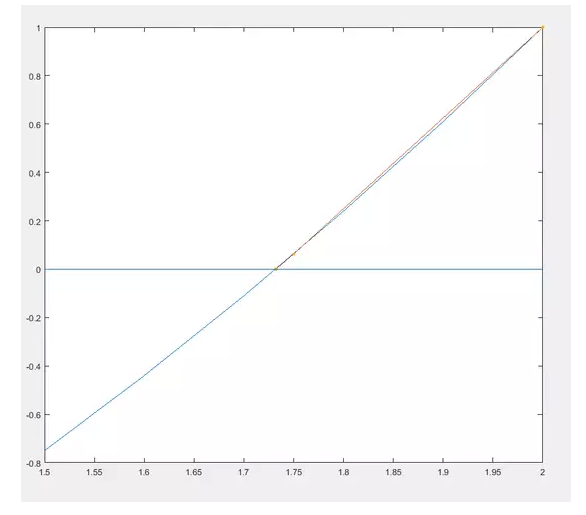
看起来两步就收敛了啊，好厉害，怎么做到不震荡的呢它?

因为每一步迭代移动切线与x轴交叉点的距离

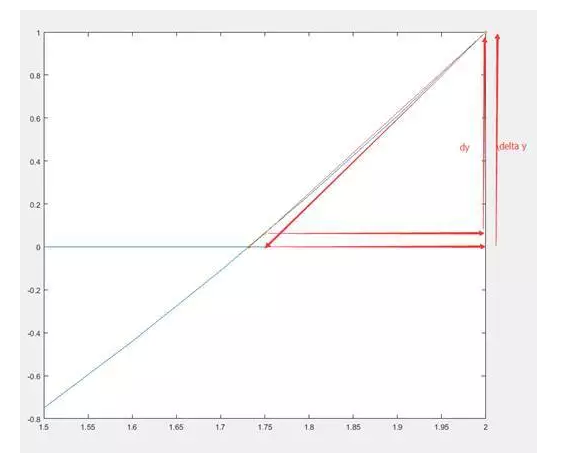
没错就是这么简单。

这里顺带一提，对于不同的方程起始点的选择也会影响迭代次数，如果有兴趣的话可以读一下 这篇文章 ，看一下神奇的0x5f375a86，2次迭代求解，这里读两次不读二次^_^

那牛顿法和极值求解有关系?看起来牛顿法只能求零点啊? Naive~~，一阶导零点不就是函数的极值或者驻点?

这个矩阵就是传说中的Hessian矩阵，不是什么拼音的简写。

还是以上面的例子解，对就是只有两个点求直线的那个，这次我们把目标函数1/2的加上。

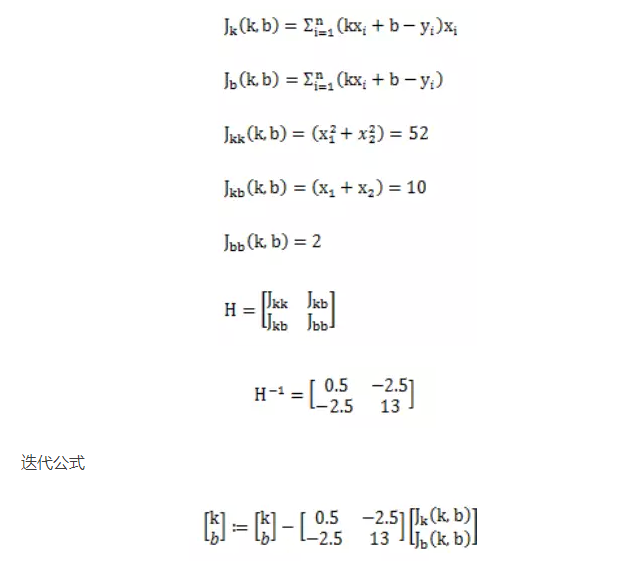
来看一下效果，看起来直接一步到位啊!!!所以牛顿法求解你们也应该知道多厉害了。

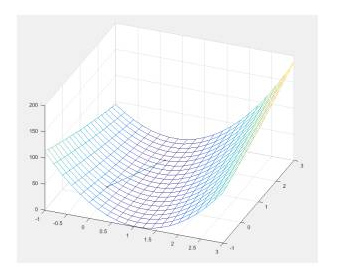
难道是我初始点选的就比较接近答案?换一个大一点的(100,100)，依然非常快!

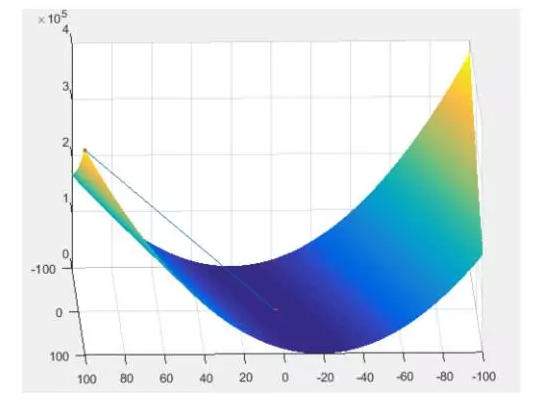
这么快的原因，可能跟方程有关，换了其他方程也许就不这样了。当然你读到这里也许会迫不及待的去找些自己想分析的数据，计算些参数，如果数据量少，几百个，没问题，几万个，还撑得住，要是直接从统计局或者人口普查中进行分析的话，算一个

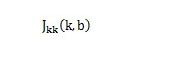
可能都很慢，而且数超大。

简单的解决办法，有一种叫做批迭代的方法，不管是在梯度计算极值还是在牛顿计算极值上都是可行的，就是假设失去大部分点对准确度没有太大的影响，比如说3个在一条直线上的点，去掉一个也没什么关系，最后反正还是会拟合成同一个参数。批迭代就是在众多的点中随机抽取一些，进行迭代计算，再随机抽取一些再进行迭代。迭代的路径可能不完美，但是最终还是会找到我们想要的答案。

商业智能与数据分析群

兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识

QQ群：81035754