资讯专栏INFORMATION COLUMN

摘要:局部最小存在,但是对于目标函数而言,它非常接近全局最小,理论研究结果表明,一些大函数可能集中于指标临界点和目标函数之间。
“为了局部泛化,我们需要所有相关变化的典型范例。”
深度学习是学习多层次的表示,相当于是多层次的抽象。如果我们能够学习这些多层次的表示,那么我们可以很好地对其泛化。
在上述(释义)总领全文陈述之后,作者提出了一些不同的人工智能(AI)策略,从以规则为基础的系统到深度学习系统,并指出在哪个层次它们的组件能够起作用。之后,他给出了从机器学习(ML)向真正人工智能迁移的3个关键点:大量数据,非常灵活的模型,强大的先验,而且,因为经典ML可以处理前两个关键点,所以他的博客是关于如果处理第三个关键点的。
在从如今的机器学习系统迈向人工智能的道路上,我们需要学习,泛化,避免维度灾难的方法,以及解决潜在解释因素的能力。在解释为什么非参数学习算法不能实现真正的人工智能之前,他首先对非参数下了详细的定义。他解释了为什么以平滑作为经典的非参数方法在高维度下不起作用,之后对维度做了如下解释:
“如果我们在数学上更深入地挖掘,我们学习到的是函数变种的数量,而不是维度的数量。在这种情况下,平滑度就是曲线中有多少上升和下降。”

“一条直线是非常平滑的。一条有升有降的曲线没那么平滑,但还是平滑的。”
所以,很显然,多带带使用平滑度并不能避免维度灾难。事实上,平滑度甚至不适用与现代的,复杂的问题,比如计算机视觉和自然语言处理。在讨论完这种有竞争力的方法(如高斯核)的失败后,Boney将目光从平滑度上转移,并解释了它的必要性:
“我们想要达到非参数,在这个意义上,我们希望随着数据的增多所有函数能灵活地扩展。在神经网络中,我们根据数据量来改变隐藏单元的个数。”
他指出,在深度学习之中,使用了2个先验,即分布式表示和深度架构。
为什么使用分布式表示?
“使用分布式表示,可以用线性参数来表示指数数量的区域。分布式表示的奇妙之处在于可以使用较少的实例来学习非常复杂的函数(有很多上升和下降的曲线)。”
在分布式表示中,特征的意义是多带带而言的,无论其他特征如何都不会改变。它们之间或许会有些互动,但是大多特征都是独立于其他特征学习得到的。Boney指出,神经网络非常善于学习表示来捕捉语义方面的东西,它们的泛化能力来源自这些表示。作为本主题的应用实例,他推荐Cristopher Olah的文章,来获取关于分布式表示和自然语言处理的知识。
对于深度的含义有许多误解
“更深的网络并不意味着有更高的生产力。更深并不意味着我们能表示更多的函数。如果我们正在尝试学习的函数有特定的特征,这些特征由许多操作的部分组成,那么使用深度神经网络来逼近这些函数可以得到更好的效果。”
之后Boney又回到原话题。他解释说,90年代后期神经网络研究被搁置(再次)的一个原因是优化问题是非凸的。80和90年代的工作成果中,神经网络在局部最小化中得到了一个指数值,同时还有内核机器的诞生,导致了神经网络的衰败,网络可能会由于不好的解决方案而失效。最近,我们有证据证明非凸问题可能不是个问题,这改变了它与神经网络的关系。
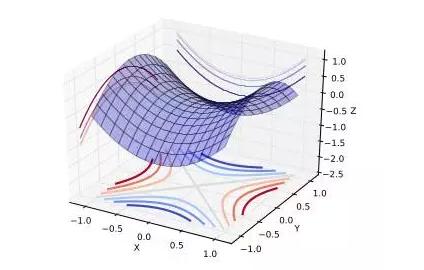
“上图展示了一个鞍点。在全局或局部最小区域,所有方向都上升,在全局或局部较大区域,所有方向都下降。”
鞍点
“我们来考虑低维度和高维度下的优化问题。在低维度中,确实存在许多局部最小。但是在高维度情况下,局部最小并不是临界点,也就是对全局来说不是关键点。当我们优化神经网络或任何高维度函数的时候,对于我们大多数优化的轨迹,临界点(点的导数是0或接近0)都是鞍点。鞍点,不像局部最小,很容易退避。”
关于鞍点的直觉是,对于靠近全局最小的局部最小,所有方向都应该是上升的;进一步下降可能性极小。局部最小存在,但是对于目标函数而言,它非常接近全局最小,理论研究结果表明,一些大函数可能集中于指标(临界点)和目标函数之间。指标相当于是各个方向上,下降的方向占所有方向的比例;如果指标不是0或1(分别是局部最小和局部较大)的,那么它是一个鞍点。
Boney继续说道,已经有经验可以验证指标和目标函数之间的关系,而没有任何证据表明神经网络优化可以得到这些结果,一些证据表明,所观察到的行为可能只是理论结果。在实践中,随机梯度下降几乎总是避开不是局部最小的表面。
这一切都表明,事实上因为鞍点的存在,局部最小可能不是问题。
Boney继续他关于鞍点的讨论,提出了一些与深度分布式表示工作的其他先验;类人学习(human learning),半监督学习,多任务学习。然后他列出了一些关于鞍点的论文。
Rinu Boney写了篇文章详细阐述深度学习的驱动力,包括对鞍点的讨论,所有的这些都很难通过简单的引用和总结来公正说明。如果想对以上讨论点进行更深的讨论,访问Boney的博客,自己读读这些具有洞察力和良好构思的文章吧。
关于译者: 刘翔宇,中通软开发工程师,关注机器学习、神经网络、模式识别。
欢迎加入本站公开兴趣群商业智能与数据分析群
兴趣范围包括各种让数据产生价值的办法,实际应用案例分享与讨论,分析工具,ETL工具,数据仓库,数据挖掘工具,报表系统等全方位知识
QQ群:81035754
文章版权归作者所有,未经允许请勿转载,若此文章存在违规行为,您可以联系管理员删除。
转载请注明本文地址:https://www.ucloud.cn/yun/4350.html
摘要:对所有参数更新时应用同样的学习率梯度由许多偏导数组成,对应着各个参数的更新。对于偏导数大的,我们希望配个小的学习率给他对于偏导数小的,我们希望配个大的学习率给他,这样各个参数都能获得大致相同的更新幅度,提高网络的健壮性。 后续【DL-CV】更高级的参数更新/优化(二) 【DL-CV】正则化,Dropout【DL-CV】浅谈GoogLeNet(咕咕net) 原版SGD的问题 原味版的S...
摘要:我认为在大多数深度学习中,算法层面上随机梯度的下降是大家所认可的。但目前似乎存在两个问题计算层面纳什平衡达不到可能会退化。 去年我一直在研究如何更好地调整GANs中的不足,但因为之前的研究方向只关注了损失函数,完全忽略了如何寻找极小值问题。直到我看到了这篇论文才有所改变:详解论文: The Numerics of GANs我参考了Mar的三层分析,并在计算层面上仔细考虑了这个问题:我们这样做...
摘要:本文将详细解析深度神经网络识别图形图像的基本原理。卷积神经网络与图像理解卷积神经网络通常被用来张量形式的输入,例如一张彩色图象对应三个二维矩阵,分别表示在三个颜色通道的像素强度。 本文将详细解析深度神经网络识别图形图像的基本原理。针对卷积神经网络,本文将详细探讨网络 中每一层在图像识别中的原理和作用,例如卷积层(convolutional layer),采样层(pooling layer),...
阅读 2629·2023-05-11 16:55
阅读 3659·2021-08-10 09:43
阅读 2772·2019-08-30 15:44
阅读 2604·2019-08-29 16:39
阅读 725·2019-08-29 13:46
阅读 2171·2019-08-29 13:29
阅读 1072·2019-08-29 13:05
阅读 837·2019-08-26 13:51