摘要：特征工程与图像处理信息检索以及表达谱等大不相同。以这种方式使用通常被称为特征提取。在这一问题的范围内，它们的直觉应该驱动特征工程处理。此外，细胞核的大小与细胞整体大小相关等等。
“特征工程”这个华丽的术语，它以尽可能容易地使模型达到良好性能的方式，来确保你的预测因子被编码到模型中。例如，如果你有一个日期字段作为一个预测因子，并且它在周末与平日的响应上有着很大的不同，那么以这种方式编码日期，它更容易取得好的效果。
但是，这取决于许多方面。
首先，它是依赖模型的。例如，如果类边界是一个对角线，那么树可能会在分类数据集上遇到麻烦，因为分类边界使用的是数据的正交分解（斜树除外）。
其次，预测编码过程从问题的特定学科知识中受益较大。在我刚才列举的例子中，你需要了解数据模式，然后改善预测因子的格式。特征工程与图像处理、信息检索以及RNA表达谱等大不相同。你需要了解关于这个问题的一些信息，并且用你的特定数据集来做好特征工作。
下面是一些训练集的数据，使用两个预测因子来建立一个二分类系统模型（我会在后面揭晓数据来源）：
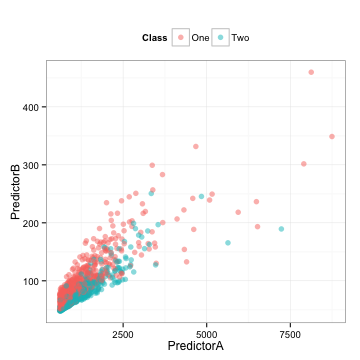
这里还有我们将在下面使用到的相关测试集。
我们可以得到以下结论：
这些数据是高度相关的（相关系数=0.85）。
每个预测因子似乎是向右倾斜的。
它们似乎是多信息的，从某种意义上来说，你或许可以画出一条对角线来区分类别。
取决于我们选择使用的模型，两个预测因子的相关性可能会困扰我们。同样，我们应该检查单个预测因子是否重要。为了衡量这一点，我们将直接使用在预测数据上的ROC曲线下方的面积。
下面是每一个预测因子的单变量盒图（在对数尺度上）：
这两个类之间有一些细微的差别，但是有很多重叠部分。预测模型A和B的ROC曲线面积分别是0.61和0.59。这个结果并不好。
那我们能做什么？主成分分析（PCA）是一种预处理的方法，它以创建新的综合预测因子（即主要成分或PC"s）的方式旋转预测数据。它通过这样的方式分析：第一个成分占预测数据中大多数（线性）变量或信息的比重。在提取第一个成分之后，第二个成分以同样的方式来处理剩下的数据，并且依次下去。对于这些数据，有两种可能的组成部分（因为只有两个预测因子）。以这种方式使用PCA通常被称为特征提取。
我们来计算下这些成分：
> library(caret)
> head(example_train)
PredictorA PredictorB Class
2 3278.726 154.89876 One
3 1727.410 84.56460 Two
4 1194.932 101.09107 One
12 1027.222 68.71062 Two
15 1035.608 73.40559 One
16 1433.918 79.47569 One
> pca_pp <- preProcess(example_train[, 1:2],
+ method = c("center", "scale", "pca"))
+ pca_pp
Call:
preProcess.default(x = example_train[, 1:2], method = c("center",
"scale", "pca"))
Created from 1009 samples and 2 variables
Pre-processing: centered, scaled, principal component signal extraction
PCA needed 2 components to capture 95 percent of the variance
> train_pc <- predict(pca_pp, example_train[, 1:2])
> test_pc <- predict(pca_pp, example_test[, 1:2])
> head(test_pc, 4)
PC1 PC2
1 0.8420447 0.07284802
5 0.2189168 0.04568417
6 1.2074404 -0.21040558
7 1.1794578 -0.20980371
请注意，我们在训练集上计算了所有的必要信息，并且将这些计算应用到测试集。那么测试集是什么样的呢？
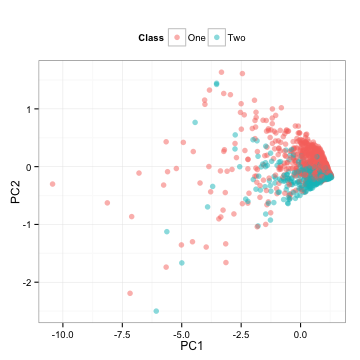
这是测试集预测因子简单的旋转。
PCA是非监督式的，这意味着当计算结束时，不需要考虑输出类。在这里，ROC曲线的下方部分，用第一个成分得到的面积是0.5，第二个成分得到的面积是0.81。这些结果与上面的点混在一起；第一个成分在类中具有随机混合的特性，而第二个成分似乎可以很好地分离类。两种成分的盒图反映了同样的情况：
在第二个成分中，两个类的分离度更高。
这很有趣。首先，尽管PCA是非监督式的，它还是成功地找到了一个新的预测因子来划分类别。其次，这些成分对于这些类别是最终要的，但对于预测器而言则没那么重要。通常PCA并不会保证任何成分会给出准确预测。但在这里，我们很幸运，它得到一个不错的预测结果。
但是，试想如果有上百个预测因子。我们可能只需要使用前X个成分来获取预测因子中绝大部分的信息，然后丢弃其他的成分。在这个例子中，第一个成分占据预测器变量的92.4%，同样的方法可能会丢弃最有效的预测因子。
特征工程的想法是怎么出现的呢？给定这两种预测因子，我们可以得到下面所示的散点图，我首先想到的事情是“有两个相关联的，正相关并且斜交的预测因子，一前一后地进行分类”。其次我想到的是“利用比例”。那么数据是什么样的呢？
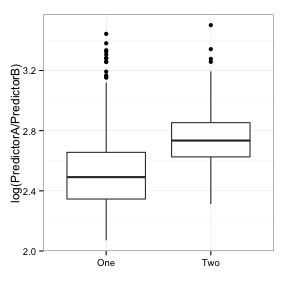
ROC曲线下方的相应面积是0.8，它跟第二个成分的结果很相近。一个基于数据视觉化探索的简单转换可能会与没有偏差的经验算法效果相当。
这些数据来自于Hill等人的细胞分割实验，预测因子A是“由旋转得到的等效圆直径的球体表面”（标记为EqSphereAreaCh1），预测因子B是细胞核的周长（PerimCh1）。一个高内涵筛选的专家，可能会自然而然的采用这两种细胞特征的比率，因为它会带来科学意义上良好的效果（我并不是那个人）。在这一问题的范围内，它们的直觉应该驱动特征工程处理。
然而，在保证诸如PCA算法效能时，机器会因此受益。总的来说，这些数据中有近60个预测因子，它们的特征和EqSphereAreaCh1相近。我的个人爱好是“基于共生矩阵像素空间排列的Haralick 结构测量”。为此研究了一段时间。问题的关键是，经常有太多的特征需要设计，而且它们很可能在一开始就很不直观。
特征提取的另一方面关系到相关性。在特定数据集上的预测因子之间往往有着高度相关性，这是很好理解的。比如，有不同的方法来量化细胞的离心率（比如拉伸程度）。此外，细胞核的大小与细胞整体大小相关等等。PCA可以显著地缓解相关性的效果。手动采用多预测因子比例的做法似乎可能不太有效，而且会花费更多的时间。
去年，在我支持的一个R&D小组中，专注于偏差分析（即建立我们预先知道的模型）和专注于非偏差分析（即让机器去寻找最优模型）的科学家之间存在着争议。我的观点处于这两者之间，认为它们之间存在一些交集。一旦挖掘完毕，机器可以将新的、有趣的特征打上“已知事物”的标签，并把它们作为知识来使用。
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/4328.html
ABSTRACT： 提出了新的换脸模型，Simple Swap（SimSwap）,可以融合任意的source face跟target face，并且保存source face的身份及target face的属性特征。模型克服了以往模型的缺陷，通过两个创新点，1，提出了ID Injection Module（IIM）模块，通过这个模块，将针对特定的source face的框架扩展到适用任意的sour...
摘要：学习笔记七数学形态学关注的是图像中的形状，它提供了一些方法用于检测形状和改变形状。学习笔记十一尺度不变特征变换，简称是图像局部特征提取的现代方法基于区域图像块的分析。本文的目的是简明扼要地说明的编码机制，并给出一些建议。 showImg(https://segmentfault.com/img/bVRJbz?w=900&h=385); 前言 开始之前，我们先来看这样一个提问： pyth...
摘要：学习笔记七数学形态学关注的是图像中的形状，它提供了一些方法用于检测形状和改变形状。学习笔记十一尺度不变特征变换，简称是图像局部特征提取的现代方法基于区域图像块的分析。本文的目的是简明扼要地说明的编码机制，并给出一些建议。 showImg(https://segmentfault.com/img/bVRJbz?w=900&h=385); 前言 开始之前，我们先来看这样一个提问： pyth...
摘要：在论文中和都设置为。得分层计算物体存在的概率，包围框回归层输出框。论文中将的阈值调为，这样对每张图片都会产生个候选区域。训练，目的是提取候选区域。这样做有两个优势。一是的数量由降为。且候选框的数量是。 1.之前框架的问题 目前的候选框提取方法通常需要提取几千个候选框，影响检测效率。RPN只提取了几百张，但是对于小物体的检测和定位仍存在问题。 2.解决问题的要点 深层次的卷积层：high...
阅读 3161·2023-04-25 20:09
阅读 3354·2022-06-28 19:00
阅读 2709·2022-06-28 19:00
阅读 2713·2022-06-28 19:00
阅读 2653·2022-06-28 19:00
阅读 2509·2022-06-28 19:00
阅读 2624·2022-06-28 19:00
阅读 2320·2022-06-28 19:00
