摘要：在上个月发表博客文章深度学习机器学习模式识别之后，博士博士后及联合创始人这一次带领我们回顾年来人工智能领域三大范式逻辑学概率方法和深度学习的演变历程。最令人兴奋的，后来的频率论与贝叶斯之争，是一些被称为概率图模型的东西。
在上个月发表博客文章《深度学习vs机器学习vs模式识别》之后，CMU博士、MIT博士后及vision.ai联合创始人Tomasz
Malisiewicz这一次带领我们回顾50年来人工智能领域三大范式（逻辑学、概率方法和深度学习）的演变历程。通过本文我们能够更深入地理解人工智能和深度学习的现状与未来。
以下为正文：
今天，我们一起来回顾过去50年人工智能（AI）领域形成的三大范式：逻辑学、概率方法和深度学习。如今，无论依靠经验和“数据驱动”的方式，还是大数据、深度学习的概念，都已经深入人心，可是早期并非如此。很多早期的人工智能方法是基于逻辑，并且从基于逻辑到数据驱动方法的转变过程受到了概率论思想的深度影响，接下来我们就谈谈这个过程。
本文按时间顺序展开，先回顾逻辑学和概率图方法，然后就人工智能和机器学习的未来走向做出一些预测。
图片来源：Coursera的概率图模型课
1.逻辑和算法（常识性的“思考”机）
许多早期的人工智能工作都是关注逻辑、自动定理证明和操纵各种符号。John McCarthy于1959年写的那篇开创性论文取名为《常识编程》也是顺势而为。
如果翻开当下最流行的AI教材之一——《人工智能：一种现代方法》（AIMA），我们会直接注意到书本开篇就是介绍搜索、约束满足问题、一阶逻辑和规划。第三版封面（见下图）像一张大棋盘（因为棋艺精湛是人类智慧的标志），还印有阿兰·图灵（计算机理论之父）和亚里士多德（最伟大的古典哲学家之一，象征着智慧）的照片。
AIMA的封面，它是CS专业本科AI课程的规范教材
然而，基于逻辑的AI遮掩了感知问题，而我很早之前就主张了解感知的原理是解开智能之谜的金钥匙。感知是属于那类对于人很容易而机器很难掌握的东西。（延伸阅读：《计算机视觉当属人工智能》，作者2011年的博文）逻辑是纯粹的，传统的象棋机器人也是纯粹算法化的，但现实世界却是丑陋的，肮脏的，充满了不确定性。
我想大多数当代人工智能研究者都认为基于逻辑的AI已经死了。万物都能完美观察、不存在测量误差的世界不是机器人和大数据所在的真实世界。我们生活在机器学习的时代，数字技术击败了一阶逻辑。站在2015年，我真是替那些死守肯定前件抛弃梯度下降的傻子们感到惋惜。
逻辑很适合在课堂上讲解，我怀疑一旦有足够的认知问题成为“本质上解决”，我们将看到逻辑学的复苏。未来存在着很多开放的认知问题，那么也就存在很多场景，在这些场景下社区不用再担心认知问题，并开始重新审视这些经典的想法。也许在2020年。
2.概率，统计和图模型（“测量”机）
概率方法在人工智能是用来解决问题的不确定性。《人工智能:一种现代方法》一书的中间章节介绍“不确定知识与推理”，生动地介绍了这些方法。如果你第一次拿起AIMA，我建议你从本节开始阅读。如果你是一个刚刚接触AI的学生，不要吝啬在数学下功夫。
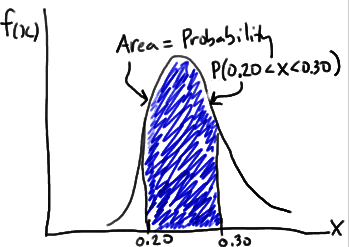
来自宾夕法尼亚州立大学的概率论与数理统计课程的PDF文件
大多数人在提到的概率方法时，都以为只是计数。外行人很容易想当然地认为概率方法就是花式计数方法。那么我们简要地回顾过去统计思维里这两种不相上下的方法。
频率论方法很依赖经验——这些方法是数据驱动且纯粹依靠数据做推论。贝叶斯方法更为复杂，并且它结合数据驱动似然和先验。这些先验往往来自第一原则或“直觉”，贝叶斯方法则善于把数据和启发式思维结合做出更聪明的算法——理性主义和经验主义世界观的完美组合。
最令人兴奋的，后来的频率论与贝叶斯之争，是一些被称为概率图模型的东西。该类技术来自计算机科学领域，尽管机器学习现在是CS和统计度的重要组成部分，统计和运算结合的时候它强大的能力才真正释放出来。
概率图模型是图论与概率方法的结合产物，2000年代中期它们都曾在机器学习研究人员中风靡一时。当年我在研究生院的时候（2005-2011），变分法、Gibbs抽样和置信传播算法被深深植入在每位CMU研究生的大脑中，并为我们提供了思考机器学习问题的一个极好的心理框架。我所知道大部分关于图模型的知识都是来自于Carlos Guestrin和Jonathan Huang。Carlos Guestrin现在是GraphLab公司（现改名为Dato）的CEO，这家公司生产大规模的产品用于图像的机器学习。Jonathan Huang现在是Google的高级研究员。
下面的视频尽管是GraphLab的概述，但它也完美地阐述了“图形化思维”，以及现代数据科学家如何得心应手地使用它。Carlos是一个优秀的讲师，他的演讲不局限于公司的产品，更多的是提供下一代机器学习系统的思路。
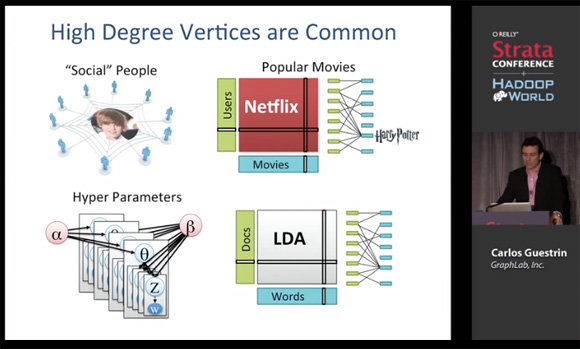
概率图模型的计算方法介绍（视频和PPT下载）
Dato CEO，Carlos Guestrin教授
如果你觉得深度学习能够解决所有机器学习问题，真得好好看看上面的视频。如果你正在构建一套推荐系统，一个健康数据分析平台，设计一个新的交易算法，或者开发下一代搜索引擎，图模型都是完美的起点。
3.深度学习和机器学习（数据驱动机）
机器学习是从样本学习的过程，所以当前较先进的识别技术需要大量训练数据，还要用到深度神经网络和足够耐心。深度学习强调了如今那些成功的机器学习算法中的网络架构。这些方法都是基于包含很多隐藏层的“深”多层神经网络。注：我想强调的是深层结构如今（2015年）不再是什么新鲜事。只需看看下面这篇1998年的“深层”结构文章。
LeNet-5，Yann LeCun开创性的论文《基于梯度学习的文档识别方法》
你在阅读LeNet模型导读时，能看到以下条款声明：
要在GPU上运行这个示例，首先得有个性能良好的GPU。GPU内存至少要1GB。如果显示器连着GPU，可能需要更多内存。
当GPU和显示器相连时，每次GPU函数调用都有几秒钟的时限。这么做是必不可少的，因为目前的GPU在进行运算时无法继续为显示器服务。如果没有这个限制，显示器将会冻结太久，计算机看上去像是死机了。若用中等质量的GPU处理这个示例，就会遇到超过时限的问题。GPU不连接显示器时就不存在这个时间限制。你可以降低批处理大小来解决超时问题。
我真的十分好奇Yann究竟是如何早在1998年就把他的深度模型折腾出一些东西。毫不奇怪，我们大伙儿还得再花十年来消化这些内容。
更新：Yann说（通过Facebook的评论）ConvNet工作可以追溯到1989年。“它有大约400K连接，并且在一台SUN4机器上花了大约3个星期训练USPS数据集（8000个训练样本）。”——LeCun
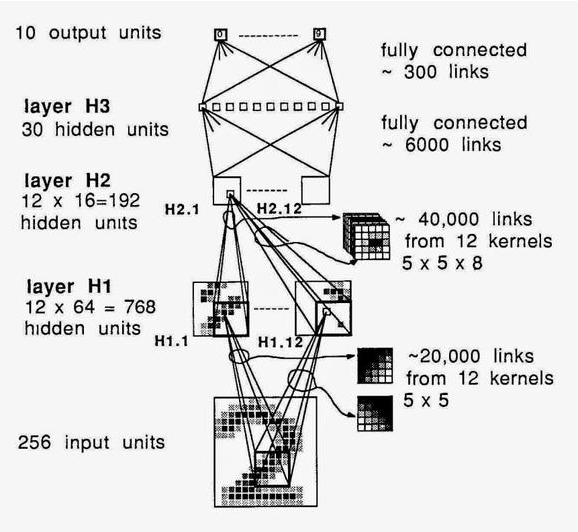
深度网络，Yann1989年在贝尔实验室的成果
注：大概同一时期（1998年左右）加州有两个疯狂的家伙在车库里试图把整个互联网缓存到他们的电脑（他们创办了一家G打头的公司）。我不知道他们是如何做到的，但我想有时候需要超前做些并不大规模的事情才能取得大成就。世界最终将迎头赶上的。
结论
我没有看到传统的一阶逻辑很快卷土重来。虽然在深度学习背后有很多炒作，分布式系统和“图形思维”对数据科学的影响更可能比重度优化的CNN来的更深远。深度学习没有理由不和GraphLab-style架构结合，未来几十年机器学习领域的重大突破也很有可能来自这两部分的结合。
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/4318.html
摘要：雅虎开源了一个进行色情图像检测的深度学习解决方案。卷积神经网络架构和权衡近年来，卷积神经网络已经在图像分类问题中取得了巨大成功。自年以来，新的卷积神经网络架构一直在不断改进标准分类挑战的精度。 雅虎开源了一个进行色情图像检测的深度学习解决方案。据文章介绍，这可能是较早的识别 NSFW 图像的开源模型。开源地址：https://github.com/yahoo/open_nsfw自动识别一张对...
摘要：这种无明确任务目标的聊天机器人也可以称作为开放领域的聊天机器人。此外，聊天机器人应该给人个性表达一致的感觉。使用深度学习技术来开发聊天机器人相对传统方法来说，整体思路非常简单并可扩展。 作者：张俊林，中科院软件所博士，技术书籍《这就是搜索引擎：核心技术详解》、《大数据日知录：架构与算法》作者。曾担任阿里巴巴、百度、新浪微博资深技术专家，目前是用友畅捷通工智能相关业务负责人，关注深度学习在自然...
摘要：机器学习是对能通过经验自动改进的计算机算法的研究。机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。 如何成为机器学习工程师https://keras-cn.readthedocs....http://www.tensorfly.cn/tfdoc... 机器学习 vs 数据分析 数据特点 数据分析 机器学习 数据类型 交易数据 行为数据 数据量 少量数据...
摘要：深度学习理论在机器翻译和字幕生成上取得了巨大的成功。在语音识别和视频，特别是如果我们使用深度学习理论来捕捉多样的时标时，会很有用。深度学习理论可用于解决长期的依存问题，让一些状态持续任意长时间。 Yoshua Bengio，电脑科学家，毕业于麦吉尔大学，在MIT和AT&T贝尔实验室做过博士后研究员，自1993年之后就在蒙特利尔大学任教，与 Yann LeCun、 Geoffrey Hinto...
摘要：在一篇论文中提到，目前深度学习算法取得好效果的主要原因归功于。最大似然估计其实目前大部分使用的损失函数都是以最大似然原理为核心而设计的。非同分布的李雅普诺夫定理大量随机因素叠加的结果，近似服从正态分布。 1. 想法 由于有朋友在北大，很高兴能蹭到深度学习的课程，李戈教授的课程十分精彩，比起只会念PPT的老师，他的教学就像在堆积知识的金字塔。 2. Loss Function 2.1 经...
阅读 369·2023-04-25 14:26
阅读 1073·2021-11-25 09:43
阅读 3239·2021-09-22 15:25
阅读 1242·2019-08-30 15:54
阅读 323·2019-08-30 12:57
阅读 608·2019-08-29 17:24
阅读 3040·2019-08-28 18:13
阅读 2474·2019-08-28 17:52
