Python完成1个全连接层的神经元网络

　　本文关键阐述了Python完成1个全连接层的神经元网络，文章内容紧扣主题进行详尽的基本介绍，具有很强的实用价值，必须的朋友可以学习一下

　　序言

　　在本文中，提前准备用Python重新开始完成1个全连接层的神经元网络。你可能会说，为何需要自己去完成，有许多库和架构能够给我们做这些事，例如Tensorflow、Pytorch等。这儿只想说仅有自己亲自完成了，就是自己的。

　　想起今日他从接触到了从事神经元网络有关工作早已是多少2、3年多，在其中也试着用tensorflow或pytorch架构去完成某些传统互联网。但是对于反向传播身后体制还是挺模糊不清。

　　梯度方向

　　梯度方向是函数公式升高更快方位，速度最快的方位换句话说正确的方向函数公式样子很险峻，那样都是函数公式减少速度最快的方位。

　　尽管有关某些基础理论、梯度消失和节点饱和状态能够伤害1个1、2、3可是细究或是没有自信，当然没有亲自动手去完成过个反向传播和完善练习全过程。所以觉得或是浮于表层，学有所用而。

　　最近这几天有段空余时间、因此运用这一段休息日即将把这一部分知识总结一下下、全面了解掌握

　　大家可能很多人都清楚训练神经网络的一个过程，便是升级网络参数，升级更新的趋势是减少交叉熵值。其实就是将学习上的问题变换因为一个改善的难题。我们该如何升级主要参数呢?我们应该测算参加练习主要参数相较于损害函数的导数，接着求得梯度方向，接着应用梯度下降法来升级主要参数，迭代更新这一过程，都可以找到1个最好解决方案来降到最低交叉熵。

　　我们都知道反向传播关键是用来清算交叉熵相较于权重值和参考点的导函数

　　或许已经听见或读到了,一些关于在互联网根据反向传播来传送误差的信息内容。再根据神经细胞的w和b对误差成就的尺寸。其实就是将误差安排到每个神经细胞上。但是这里的误差(error)是什么意思呀？这一误差的准确的界定到底是什么呢？答案就是这种误差是通过每层神经元网络所成就的，并且某一层楼误差是后续层误差前提下平摊的，网络里第层误差用以表明。

　　反向传播都是基于4个基本方程的，通过这个方程式来数据误差和交叉熵，这儿把这4个方程式一一列举

　　对于如何讲解这一4个方程式，接着想要1期共享来阐述。

　　classNeuralNetwork(object):
　　def__init__(self):
　　pass
　　defforward(self,x):
　　#回到前向传播的Z可能就是w和b特征函数，键入激活函数前的值
　　#回到激活函数伤害值A
　　#z_s,a_s
　　pass
　　defbackward(self,y,z_s,a_s):
　　#回到前向传播中学到参数导函数dwdb
　　pass
　　deftrain(self,x,y,batch_size=10,epochs=100,lr=0.001):
　　pass

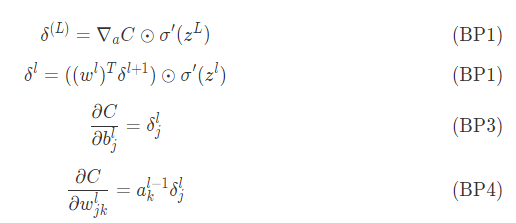
　　我们是神经网络学习全过程，其实就是练习全过程。主要分两阶段前向传播和后向传播

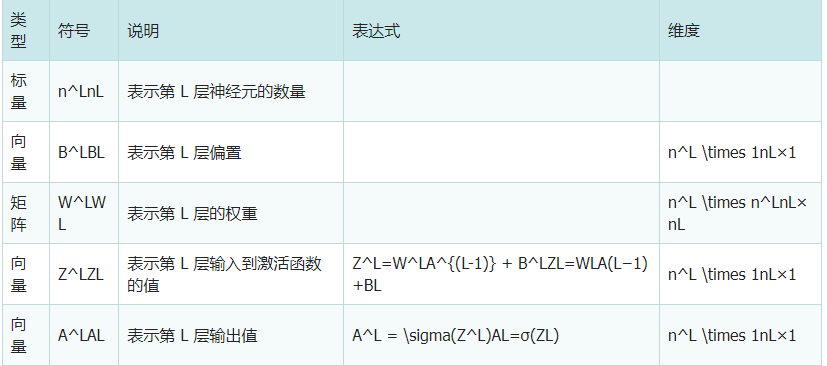
　　在前向传播函数中，关键测算传递的Z和A，有关Z和A指的是什么请参阅前边报表

　　在反向传播中测算可学习培训自变量w和b的导函数

　　def__init__(self,layers=[2,10,1],activations=['sigmoid','sigmoid']):
　　assert(len(layers)==len(activations)+1)
　　self.layers=layers
　　self.activations=activations
　　self.weights=[]
　　self.biases=[]
　　foriinrange(len(layers)-1):
　　self.weights.append(np.random.randn(layers[i+1],layers))
　　self.biases.append(np.random.randn(layers[i+1],1))

　　layers主要参数用以特定每层神经细胞的数量

　　activations为每层特定激活函数，其实就是

　　来简易解悉一下下编码assert(len(layers)==len(activations)+1)

　　foriinrange(len(layers)-1):
　　self.weights.append(np.random.randn(layers[i+1],layers))
　　self.biases.append(np.random.randn(layers[i+1],1))
　　因为权重值连接每个层神经细胞的w和b，可能就两两层之间的方程式，上面编码是对
　　前向传播
　　deffeedforward(self,x):
　　#回到前向传播的值
　　a=np.copy(x)
　　z_s=[]
　　a_s=[a]
　　foriinrange(len(self.weights)):
　　activation_function=self.getActivationFunction(self.activations)
　　z_s.append(self.weights.dot(a)+self.biases)
　　a=activation_function(z_s[-1])
　　a_s.append(a)
　　return(z_s,a_s)

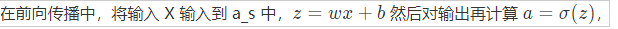
　　这里激活函数，这个函数返回值是一个函数，在python用lambda来返回一个函数，这里简答留下一个伏笔，随后会对其进行修改。

　　staticmethod
　　def getActivationFunction(name):
　　if(name=='sigmoid'):
　　return lambda x:np.exp(x)/(1+np.exp(x))
　　elif(name=='linear'):
　　return lambda x:x
　　elif(name=='relu'):
　　def relu(x):
　　y=np.copy(x)
　　y[y<0]=0
　　return y
　　return relu
　　else:
　　print('Unknown activation function.linear is used')
　　return lambda x:x
　　[staticmethod]
　　def getDerivitiveActivationFunction(name):
　　if(name=='sigmoid'):
　　sig=lambda x:np.exp(x)/(1+np.exp(x))
　　return lambda x:sig(x)*(1-sig(x))
　　elif(name=='linear'):
　　return lambda x:1
　　elif(name=='relu'):
　　def relu_diff(x):
　　y=np.copy(x)
　　y[y>=0]=1
　　y[y<0]=0
　　return y
　　return relu_diff
　　else:
　　print('Unknown activation function.linear is used')
　　return lambda x:1

　　反向传播

　　这是本次分享重点

　　def backpropagation(self,y,z_s,a_s):
　　dw=[]#dC/dW
　　db=[]#dC/dB
　　deltas=[None]*len(self.weights)#delta=dC/dZ计算每一层的误差
　　#最后一层误差
　　deltas[-1]=((y-a_s[-1])*(self.getDerivitiveActivationFunction(self.activations[-1]))(z_s[-1]))
　　#反向传播
　　for i in reversed(range(len(deltas)-1)):
　　deltas<i>=self.weights[i+1].T.dot(deltas[i+1])*(self.getDerivitiveActivationFunction(self.activations<i>)(z_s<i>))
　　#a=[print(d.shape)for d in deltas]
　　batch_size=y.shape[1]
　　db=[d.dot(np.ones((batch_size,1)))/float(batch_size)for d in deltas]
　　dw=[d.dot(a_s<i>.T)/float(batch_size)for i,d in enumerate(deltas)]
　　#返回权重(weight)矩阵and偏置向量(biases)
　　return dw,db

　　综上所述，这篇文章就给大家介绍到这里了，希望可以给大家带来一定的帮助。