python图像处理之边沿轮廊检验

89542767 发布于2022-12-25 16:10 / 586人阅读

　　此篇文章主要是详细介绍了python图像处理之边沿轮廊检验实例详细说明，感兴趣的小伙伴可以参考借鉴一下，希望可以有一定的帮助，祝愿大家多多的发展，尽早涨薪

　　前言

　　在前的python图像处理简易过滤中，己经介绍了许多算法用于检验边沿，在其中用到较多的canny算法图像分割。

　　这篇大家介绍某些其他方式来测试轮廊。

　　1、搜索轮廊（find_contours)

　　measure控制模块中的find_contours()函数公式，主要用来检验灰度图像边缘轮廊。

　　函数原型为：

　　skimage.measure.find_contours(array,level)

　　array:一种二值二维数组图象

　　level:在源图像搜索轮廊的等级值

　　回到轮廊目录结合，能用for循环取下每条轮廊。

　　例1：

</>复制代码 
　　importnumpyasnp
　　importmatplotlib.pyplotasplt
　　fromskimageimportmeasure,draw
　　#生成二值测试图像
　　img=np.zeros([100,100])
　　img[20:40,60:80]=1#矩形
　　rr,cc=draw.circle(60,60,10)#小圆
　　rr1,cc1=draw.circle(20,30,15)#大圆
　　img[rr,cc]=1
　　img[rr1,cc1]=1
　　#检测所有图形的轮廓
　　contours=measure.find_contours(img,0.5)
　　#绘制轮廓
　　fig,(ax0,ax1)=plt.subplots(1,2,figsize=(8,8))
　　ax0.imshow(img,plt.cm.gray)
　　ax1.imshow(img,plt.cm.gray)
　　forn,contourinenumerate(contours):
　　ax1.plot(contour[:,1],contour[:,0],linewidth=2)
　　ax1.axis('image')
　　ax1.set_xticks([])
　　ax1.set_yticks([])
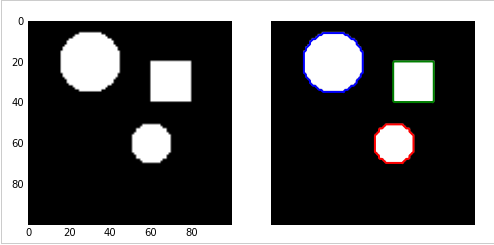
　　plt.show()

　　结果如下：不同的轮廓用不同的颜色显示

</>复制代码 
　　importmatplotlib.pyplotasplt
　　fromskimageimportmeasure,data,color
　　#生成二值测试图像
　　img=color.rgb2gray(data.horse())
　　#检测所有图形的轮廓
　　contours=measure.find_contours(img,0.5)
　　#绘制轮廓
　　fig,axes=plt.subplots(1,2,figsize=(8,8))
　　ax0,ax1=axes.ravel()
　　ax0.imshow(img,plt.cm.gray)
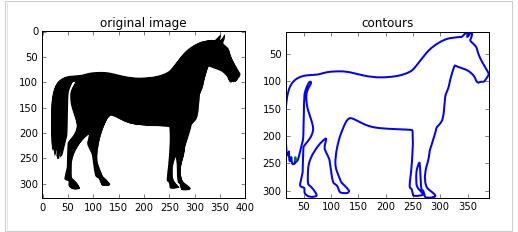
　　ax0.set_title('originalimage')
　　rows,cols=img.shape
　　ax1.axis([0,rows,cols,0])
　　forn,contourinenumerate(contours):
　　ax1.plot(contour[:,1],contour[:,0],linewidth=2)
　　ax1.axis('image')
　　ax1.set_title('contours')
　　plt.show()

　2、逼近多边形曲线

　　逼近多边形曲线有两个函数：subdivide_polygon（)和approximate_polygon（）

　　subdivide_polygon（)采用B样条（B-Splines)来细分多边形的曲线，该曲线通常在凸包线的内部。

　　函数格式为：

　　skimage.measure.subdivide_polygon(coords,degree=2,preserve_ends=False)

　　coords:坐标点序列。

　　degree:B样条的度数，默认为2

　　preserve_ends:如果曲线为非闭合曲线，是否保存开始和结束点坐标，默认为false

　　返回细分为的坐标点序列。

　　approximate_polygon（）是基于Douglas-Peucker算法的一种近似曲线模拟。它根据指定的容忍值来近似一条多边形曲线链，该曲线也在凸包线的内部。

　　函数格式为:

　　skimage.measure.approximate_polygon(coords,tolerance)

　　coords:坐标点序列

　　tolerance:容忍值

　　返回近似的多边形曲线坐标序列。

　　例：

</>复制代码 
　　importnumpyasnp
　　importmatplotlib.pyplotasplt
　　fromskimageimportmeasure,data,color
　　#生成二值测试图像
　　hand=np.array([[1.64516129,1.16145833],
　　[1.64516129,1.59375],
　　[1.35080645,1.921875],
　　[1.375,2.18229167],
　　[1.68548387,1.9375],
　　[1.60887097,2.55208333],
　　[1.68548387,2.69791667],
　　[1.76209677,2.56770833],
　　[1.83064516,1.97395833],
　　[1.89516129,2.75],
　　[1.9516129,2.84895833],
　　[2.01209677,2.76041667],
　　[1.99193548,1.99479167],
　　[2.11290323,2.63020833],
　　[2.2016129,2.734375],
　　[2.25403226,2.60416667],
　　[2.14919355,1.953125],
　　[2.30645161,2.36979167],
　　[2.39112903,2.36979167],
　　[2.41532258,2.1875],
　　[2.1733871,1.703125],
　　[2.07782258,1.16666667]])
　　#检测所有图形的轮廓
　　new_hand=hand.copy()
　　for_inrange(5):
　　new_hand=measure.subdivide_polygon(new_hand,degree=2)
　　#approximatesubdividedpolygonwithDouglas-Peuckeralgorithm
　　appr_hand=measure.approximate_polygon(new_hand,tolerance=0.02)
　　print("Numberofcoordinates:",len(hand),len(new_hand),len(appr_hand))
　　fig,axes=plt.subplots(2,2,figsize=(9,8))
　　ax0,ax1,ax2,ax3=axes.ravel()
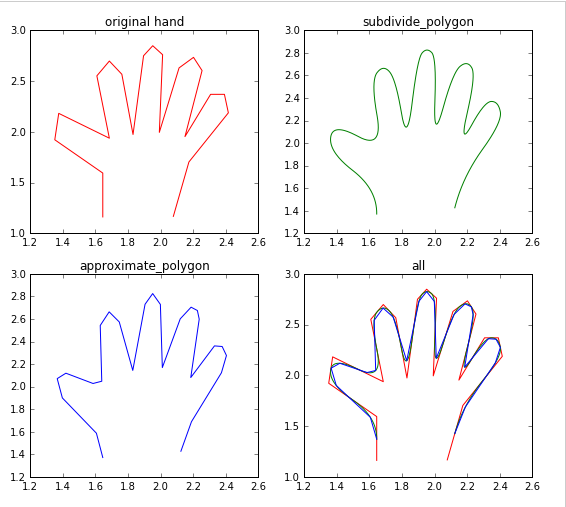
　　ax0.plot(hand[:,0],hand[:,1],'r')
　　ax0.set_title('originalhand')
　　ax1.plot(new_hand[:,0],new_hand[:,1],'g')
　　ax1.set_title('subdivide_polygon')
　　ax2.plot(appr_hand[:,0],appr_hand[:,1],'b')
　　ax2.set_title('approximate_polygon')
　　ax3.plot(hand[:,0],hand[:,1],'r')
　　ax3.plot(new_hand[:,0],new_hand[:,1],'g')
　　ax3.plot(appr_hand[:,0],appr_hand[:,1],'b')
　　ax3.set_title('all')

综上所述，这篇文章就给大家介绍到这里了，希望可以给大家带来帮助。

GPU云服务器云服务器 python统计检验 python t检验 Python 之字符串表单检验

文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。

转载请注明本文地址：https://www.ucloud.cn/yun/128805.html

【基础知识】水平触发与边沿触发

摘要：一基础水平触发基本概念读缓冲区不为空时读事件触发。开启时，会把监听套接字所有可读的事件全部读取，此时可以使用边沿触发。但为了保证连接不丢失，仍然采用水平触发通信套接字设置对于与客户端通信使用的套接字默认使用水平触发。一. 基础 1.1 水平触发基本概念读缓冲区不为空时, 读事件触发。写缓冲区不为满时, 写事件触发。处理流程 accept新的连接, 监听读事件。读事件到达, 处理读...

MrZONT 2019-07-25 14:32 评论0 收藏0
痞子衡嵌入式：嵌入式Cortex-M系统中断延迟及其测量方法简介

摘要：今天痞子衡给大家分享的是系统中断延迟及其测量方法。至此，系统中断延迟及其测量方法痞子衡便介绍完毕了，掌声在哪里欢迎订阅欢迎订阅文章会同时发布到我的博客园主页主页知乎主页微信公众号平台上。　　大家好，我是痞子衡，是正经搞技术的痞子。今天痞子衡给大家分享的是Cortex-M系统中断延迟及其测量方法。　　在嵌入式领域里，实时性是个经常被我们挂在嘴边的概念，这里的实时性主要强调得是当外界事件发生时，...

不知名网友 2021-11-26 11:11 评论0 收藏0
SPI总线协议

摘要：目录概述概述总线机制总线机制的四种工作模式的四种工作模式数据交换数据交换概述是一种同步串行通信协议，由一个主设备和一个或多个从设备组成，主设备启动与从设备的同步通信，从而完成数据的交换。目录 1.SPI概述 2.SPI总线机制 3.SPI的四种工作模式 4.SPI数据交换 1.SPI概述...

Travis 2021-10-09 09:43 评论0 收藏0
Programming Computer Vision with Python （学习笔记五）

摘要：下面是二维空间的高斯分布函数公式这个公式被称作高斯核。高斯模糊使用高斯平均算子来实现的图像模糊叫高斯模糊，也叫高斯平滑被认为是一种最优的图像平滑处理。 SciPy库 SciPy库，与之前我们使用的NumPy和Matplotlib，都是scipy.org提供的用于科学计算方面的核心库。相对NumPy，SciPy库提供了面向更高层应用的算法和函数(其实也是基于NumPy实现的），并以子模块...

Rocko 2019-07-31 10:49 评论0 收藏0