资讯专栏INFORMATION COLUMN

小编写这篇文章的主要目的,主要是来给大家去做出一个相关性的介绍,介绍的内容主要还是涉及到Python pyecharts,主要是利用Python pyecharts去绘制漏斗,那么,具体要怎么绘制呢?下面给大家详细解答下。
漏斗图
漏斗图是由Light等在1984年提出,一般以单个研究的效应量为横坐标,样本含量为纵坐标做的散点图。效应量可以为RR、OR和死亡比或者其对数值等。理论上讲,被纳入Meta分析的各独立研究效应的点估计,在平面坐标系中的集合应为一个倒置的漏斗形,因此称为漏斗图。
样本量小,研究精度低,分布在漏斗图的底部,向周围分散;
样本量大,研究精度高,分布在漏斗图的顶部,向中间集中。
漏斗图法的优点是:
简单易行,只需要被纳入的独立研究的样本含量和效应量便可绘制。
漏斗图法的缺点是:
漏斗图的对称仅通过目测,无严格限定,不同观察者可能有不同的结果;
漏斗图只能对发表偏倚进行粗略的定性判断,特别是在被纳入的独立研究个数较少时,又增加了判断漏斗图中散点是否存在对称性的难度;
可以使系统评价人员意识到存在的问题,但不能提供解决方法。
漏斗图系列模板
尖顶型漏斗图
数据可以通过Python进行预处理然后导入模板进行绘制。
from pyecharts import options as opts
from pyecharts.charts import Funnel
from pyecharts.faker import Faker
c=(
Funnel()
.add(
"类别",
[list(z)for z in zip(Faker.choose(),Faker.values())],
sort_="ascending",
label_opts=opts.LabelOpts(position="inside"),
)
.set_global_opts(title_opts=opts.TitleOpts(title="标题"))
.render("尖顶型漏斗.html")
)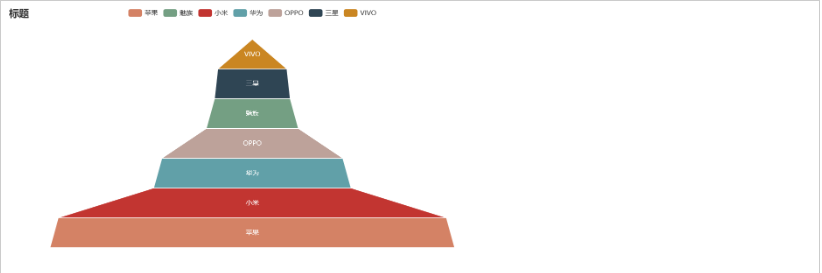
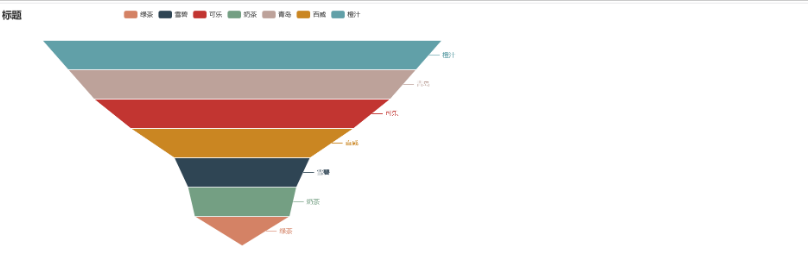
锥子型漏斗
只需要把数据进行一定的排序就好了,当然在日常的科研统计分析肯定不是简单的数据。
from pyecharts import options as opts
from pyecharts.charts import Funnel
from pyecharts.faker import Faker
c=(
Funnel()
.add("类别",[list(z)for z in zip(Faker.choose(),Faker.values())])
.set_global_opts(title_opts=opts.TitleOpts(title="标题"))
.render("锥子型漏斗.html")
)
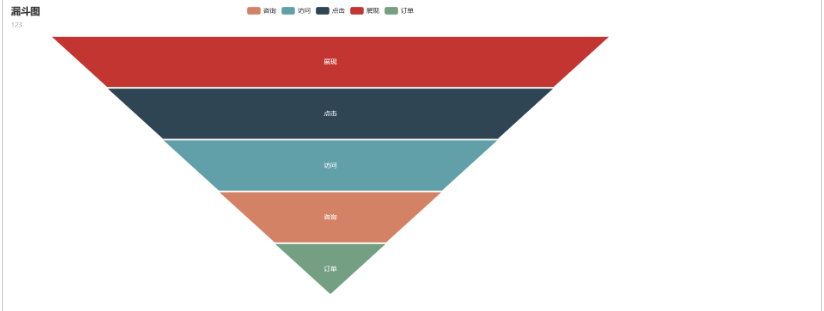
三角形漏斗
import pyecharts.options as opts
from pyecharts.charts import Funnel
x_data=["展现","点击","访问","咨询","订单"]
y_data=[100,80,60,40,20]
data=[[x_data<i>,y_data<i>]for i in range(len(x_data))]
(
Funnel(init_opts=opts.InitOpts(width="1200px",height="600px"))
.add(
series_name="",
data_pair=data,
gap=2,
tooltip_opts=opts.TooltipOpts(trigger="item",formatter="{a}<br/>{b}:{c}%"),
label_opts=opts.LabelOpts(is_show=True,position="inside"),
itemstyle_opts=opts.ItemStyleOpts(border_color="#fff",border_width=1),
)
.set_global_opts(title_opts=opts.TitleOpts(title="漏斗图",subtitle="123"))
.render("三角形漏斗.html")
)
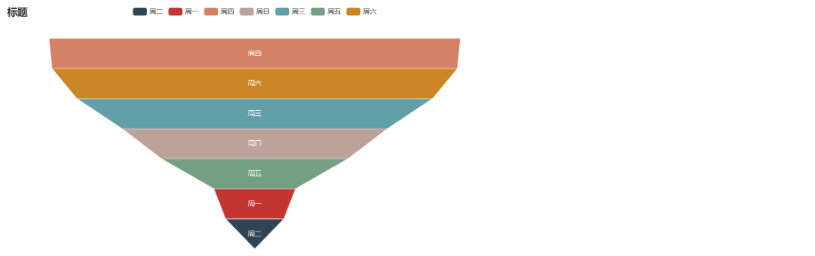
连接型漏斗
from pyecharts import options as opts
from pyecharts.charts import Funnel
from pyecharts.faker import Faker
c=(
Funnel()
.add(
"类别",
[list(z)for z in zip(Faker.choose(),Faker.values())],
label_opts=opts.LabelOpts(position="inside"),
)
.set_global_opts(title_opts=opts.TitleOpts(title="标题"))
.render("连接型漏斗.html")
)
综上所述,这篇文章就给大家介绍完毕了,希望可以给大家带来更多帮助。
文章版权归作者所有,未经允许请勿转载,若此文章存在违规行为,您可以联系管理员删除。
转载请注明本文地址:https://www.ucloud.cn/yun/128292.html
Python pyecharts作为常用的数据可视化软件,能够清晰的将海量的数据,去做一个拆分,要是更直观的去查看数据图表的话,就需要去制作云图了?那么,怎么制作云图呢?下面就给大家详细的做个解答。 词云图 什么是词云图,相信大家肯定不会感到陌生,一本书统计里面出现的词频,然后可视化展示,让读者快速的了解这个主题纲要,这就是词云的直接效果。 词云图系列模板 固定模式词云图 修改一些参...
这篇文章介绍的主要内容是,利用Python pyecharts去绘制柱状图,涉及到内容知识点还是比较的多的,那么,具体需要怎么操作呢?下面就给大家以案例的形式,去做一个介绍,大家仔细的阅读下。 主题介绍 pyecharts里面有很多的主题可以供我们选择,我们可以根据自己的需要完成主题的配置,这样就告别了软件的限制,可以随意的发挥自己的艺术细胞了。 图表参数 '''...
小编写这篇文章的主要目的,主要还是去进行讲解一些关于Python pyecharts绘制仪表盘的一些讲解,具体怎么去进行操作呢?下面就给大家详细解答下。 仪表盘 仪表盘的效果我只能说炫酷而已,如果想要运用在实际的场景中,我其实也不清楚那个场景比较适合,但是pyecharts毕竟是炫酷可视化的利器,炫酷自然也就有它了。 小汽车仪表盘是长这样的,下面我们来看看pyecharts的仪表盘是怎么...
小编写这篇文章的主要目的,主要是给大家去做一个解答,解答的内容主要是关于Python pyecharts的一些案例,包括如何使用它去进行绘制一个相关的散点图,怎么能够快速的去进行绘制。就具体的内容,下面就给大家详细解答下。 什么是散点图? 散点图是指在数理统计回归分析中,数据点在直角坐标系平面上的分布图,散点图表示因变量随自变量而变化的大致趋势,由此趋势可以选择合适的函数进行经验分布的拟合...
小编写这篇文章的主要目的,主要是给大家去做一个详细解答,介绍的内容是关于Python pyecharts的一些详细内容,给大家讲解关于如何绘制水球图等相关事宜,具体的内容,下面给大家详细解答。 水球图 水球图首先是动态的效果,像水流一样波动,所以看起来比较的舒服,一般用于业务里面的完成率,其实和之前的仪表盘有点类似,但是我个人绝对水球图更加的好,因为看起来比较的炫酷。 frompyech...
阅读 1046·2023-01-14 11:38
阅读 1042·2023-01-14 11:04
阅读 874·2023-01-14 10:48
阅读 2332·2023-01-14 10:34
阅读 1117·2023-01-14 10:24
阅读 1009·2023-01-14 10:18
阅读 636·2023-01-14 10:09
阅读 711·2023-01-14 10:02