Python可视化神器pyecharts绘制箱型图的方法

　　小编写这篇文章的主要目的，主要是给大家做一个详细的介绍，介绍的内容是Python可视化神器，这个神器指的是pyecharts，那么，怎么样利用这种语言去进行绘制箱型图呢？下面小编就给大家详细解答下。

　　概念

　　后面的图形都是一些专业的统计图形，当然也会是我们可视化的对象。

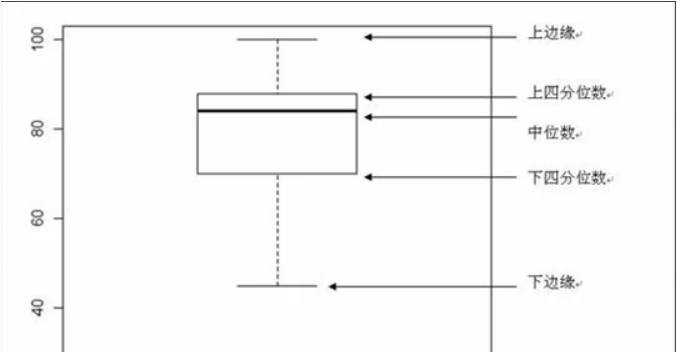
　　箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用，常见于品质管理。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后，连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。

　　用处

　　1.直观明了地识别数据批中的异常值

　　上文讲了很久的识别异常值，其实箱线图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不会影响箱形图的数据形状，箱线图识别异常值的结果比较客观。由此可见，箱线图在识别异常值方面有一定的优越性。

　　2.利用箱线图判断数据批的偏态和尾重

　　对于标准正态分布的样本，只有极少值为异常值。异常值越多说明尾部越重，自由度越小（即自由变动的量的个数）；

　　而偏态表示偏离程度，异常值集中在较小值一侧，则分布呈左偏态；异常值集中在较大值一侧，则分布呈右偏态。

　　3.利用箱线图比较几批数据的形状

　　同一数轴上，几批数据的箱线图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。如上图，可直观得看出第三季度各分公司的销售额大体都在下降。

　　箱形图系列模板

　　第一个箱形图

　　说实话这类图形的绘制，如果不懂专业的知识可能也无法理解，对于如何深层次的理解这个图形的具体含义，请移步到其他专栏，我会详细介绍，这里就不做过多的解释了。

　　from pyecharts import options as opts
　　from pyecharts.charts import Boxplot
　　v1=[
　　[850,740,900,1070,930,850,950,980,980,880,1000,980],
　　[960,940,960,940,880,800,850,880,900,840,830,790],
　　]
　　v2=[
　　[890,810,810,820,800,770,760,740,750,760,910,920],
　　[890,840,780,810,760,810,790,810,820,850,870,870],
　　]
　　c=Boxplot()
　　c.add_xaxis(["expr1","expr2"])
　　c.add_yaxis("A",c.prepare_data(v1))
　　c.add_yaxis("B",c.prepare_data(v2))
　　c.set_global_opts(title_opts=opts.TitleOpts(title="标题"))
　　c.render("简单示例.html")
　　print(c.prepare_data(v1))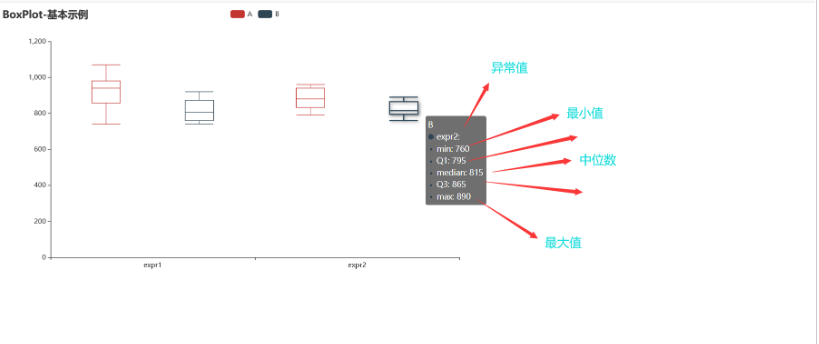

   　复杂一点的图例

　　import pyecharts.options as opts
　　from pyecharts.charts import Grid,Boxplot,Scatter
　　y_data=[
　　[
　　850,
　　740,
　　900,
　　1070,
　　930,
　　850,
　　950,
　　980,
　　980,
　　880,
　　1000,
　　980,
　　930,
　　650,
　　760,
　　810,
　　1000,
　　1000,
　　960,
　　960,
　　],
　　[
　　960,
　　940,
　　960,
　　940,
　　880,
　　800,
　　850,
　　880,
　　900,
　　840,
　　830,
　　790,
　　810,
　　880,
　　880,
　　830,
　　800,
　　790,
　　760,
　　800,
　　],
　　[
　　880,
　　880,
　　880,
　　860,
　　720,
　　720,
　　620,
　　860,
　　970,
　　950,
　　880,
　　910,
　　850,
　　870,
　　840,
　　840,
　　850,
　　840,
　　840,
　　840,
　　],
　　[
　　890,
　　810,
　　810,
　　820,
　　800,
　　770,
　　760,
　　740,
　　750,
　　760,
　　910,
　　920,
　　890,
　　860,
　　880,
　　720,
　　840,
　　850,
　　850,
　　780,
　　],
　　[
　　890,
　　840,
　　780,
　　810,
　　760,
　　810,
　　790,
　　810,
　　820,
　　850,
　　870,
　　870,
　　810,
　　740,
　　810,
　　940,
　　950,
　　800,
　　810,
　　870,
　　],
　　]
　　scatter_data=[650,620,720,720,950,970]
　　box_plot=Boxplot()
　　box_plot=(
　　box_plot.add_xaxis(xaxis_data=["expr 0","expr 1","expr 2","expr 3","expr 4"])
　　.add_yaxis(series_name="",y_axis=box_plot.prepare_data(y_data))
　　.set_global_opts(
　　title_opts=opts.TitleOpts(
　　pos_left="center",title="Michelson-Morley Experiment"
　　),
　　tooltip_opts=opts.TooltipOpts(trigger="item",axis_pointer_type="shadow"),
　　xaxis_opts=opts.AxisOpts(
　　type_="category",
　　boundary_gap=True,
　　splitarea_opts=opts.SplitAreaOpts(is_show=False),
　　axislabel_opts=opts.LabelOpts(formatter="expr{value}"),
　　splitline_opts=opts.SplitLineOpts(is_show=False),
　　),
　　yaxis_opts=opts.AxisOpts(
　　type_="value",
　　name="km/s minus 299,000",
　　splitarea_opts=opts.SplitAreaOpts(
　　is_show=True,areastyle_opts=opts.AreaStyleOpts(opacity=1)
　　),
　　),
　　)
　　.set_series_opts(tooltip_opts=opts.TooltipOpts(formatter="{b}:{c}"))
　　)
　　scatter=(
　　Scatter()
　　.add_xaxis(xaxis_data=["expr 0","expr 1","expr 2","expr 3","expr 4"])
　　.add_yaxis(series_name="",y_axis=scatter_data)
　　.set_global_opts(
　　title_opts=opts.TitleOpts(
　　pos_left="10%",
　　pos_top="90%",
　　title="upper:Q3+1.5*IQRnlower:Q1-1.5*IQR",
　　title_textstyle_opts=opts.TextStyleOpts(
　　border_color="#999",border_width=1,font_size=14
　　),
　　),
　　yaxis_opts=opts.AxisOpts(
　　axislabel_opts=opts.LabelOpts(is_show=False),
　　axistick_opts=opts.AxisTickOpts(is_show=False),
　　),
　　)
　　)
　　grid=(
　　Grid(init_opts=opts.InitOpts(width="1200px",height="600px"))
　　.add(
　　box_plot,
　　grid_opts=opts.GridOpts(pos_left="10%",pos_right="10%",pos_bottom="15%"),
　　)
　　.add(
　　scatter,
　　grid_opts=opts.GridOpts(pos_left="10%",pos_right="10%",pos_bottom="15%"),
　　)
　　.render("第一个箱形图.html")
　　)

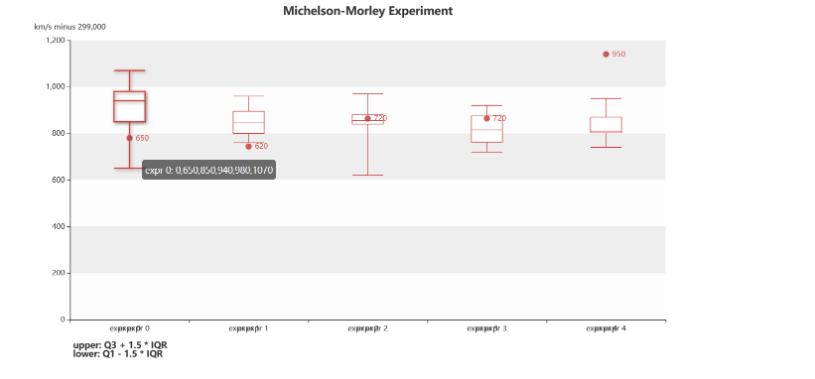
　　其实对于这个图形的绘制我个人觉得掌握好一定技巧，绘制图形并不难，主要是你要知道一定数据分析方法，不然空谈数据可视也是枉然。

　　综上所述，这篇文章就给大家介绍到这里了，希望可以给大家带来更多帮助。