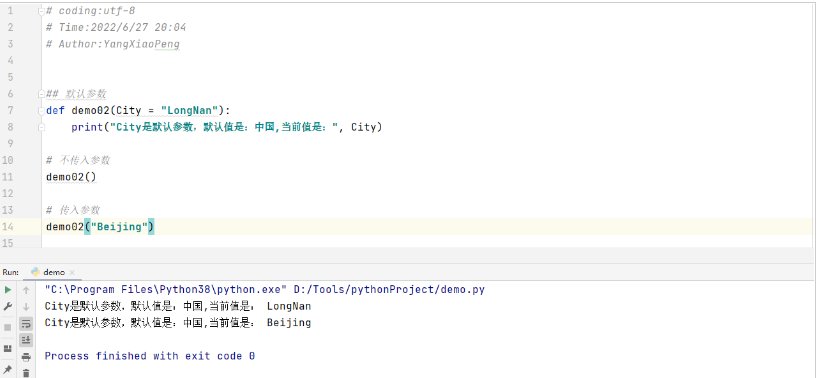
小编写这篇文章的主要目的，是用来给大家介绍关于Python中代码的相关实例，比如教大家怎么用Python计算AUC代码，具体代码内容，下面给大家一一列举出来。
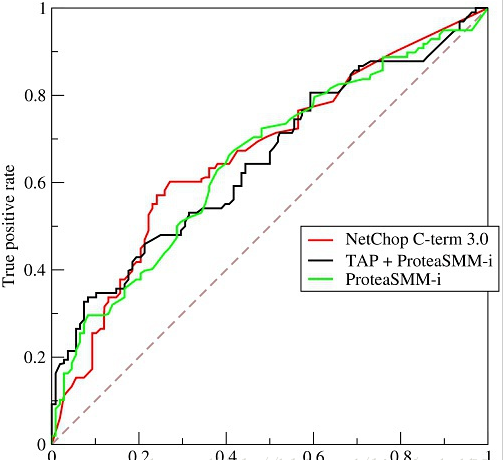
AUC是人工智能中常用的评级判定手段，它的具体意义是什么呢？看下图：
下面的表格给大家做出了具体的解释
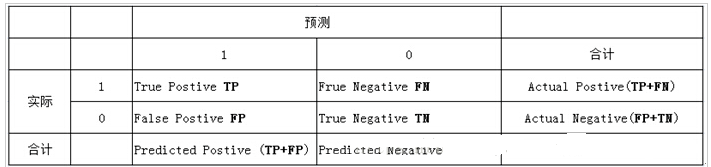
表中列代表预测分类，行代表实际分类：
实际1，预测1：真正类（tp）
实际1，预测0：假负类（fn）
实际0，预测1：假正类（fp）
实际0，预测0：真负类（tn）
真实负样本总数=n=fp+tn
真实正样本总数=p=tp+fn
在第一张图中，
横坐标false positive rate代表假正类率，由fp/n计算得到，
意为在实际负样本中出现预测正样本的概率。
纵坐标true positive rate代表真正类率，由tp/p计算得到，
意为在实际正样本中出现预测正样本的概率。
为什么指标可以衡量分类效果？
下面解释下这条曲线内容
1、通过分类器，测试其概率，然后从高到低做一个排序
2.由上到小，分别以每一个预测概率作为阈值，大于该阈值的认定其为1，小于的为0，计算fp rate和tp rate。
对于一个有分类效果（效果比随机要好）的分类器，刚开始将高概率作为阈值时，阈值以上的的话，可以做出一个平均值;阈值以上的假正样本占全部负样本的比例（fp rate）。
auc理解
auc就是：随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率。
AUC计算
方法一
在有k个正样本数据,p个负样本的数据集里。一共有k*l对样本（一对样本即，一个正样本与一个负样本）。统计这k*l对样本里，来预判其相关的一个概率值。
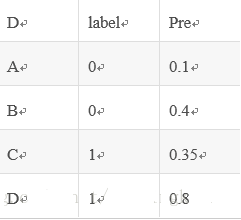
举个例子：
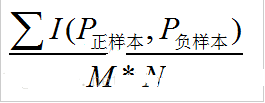
假设有4条样本。2个正样本，2个负样本，那么M*N=4。
即总共有4个样本对。分别是：
（D,B）,（D,A）,(C,B),（C,A）。
在（D,B）样本对中，正样本D预测的概率大于负样本B预测的概率（也就是D的得分比B高），记为1
同理，对于（C,B）。正样本C预测的概率小于负样本C预测的概率，记为0.
那么auc如下：
假如出现得分一致的时候：
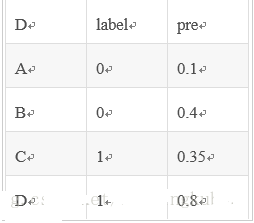
同样本是4个样本对，对于样本对（C,B）其I值为0.5。
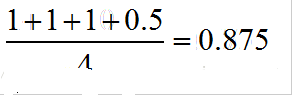
方法二
利公式：
对预测概率做一个从上到下的排序
对其中的概率数值设一个rank值（最高的概率的rank为n,第二高的为n-1）
rank实际上代表了该score（预测概率）超过的样本的数目
为了求证正样本的score值大于负样本，假如说有正向容量，那么，其相关的值，任意组合起来的话，都是比较大的了。我们取它的rank值为k，但是k-1中有M-1是正样例和正样例的组合这种是不在统计范围内的（为计算方便我们取n组，相应的不符合的有M个），所以要减掉，那么同理排在第二位的k-1，会有M-1个是不满足的，依次类推，故得到后面的公式M*(M+1)/2，我们可以验证在正样本score都大于负样本的假设下，AUC的值为1
除以M*k
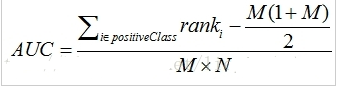
举例说明：
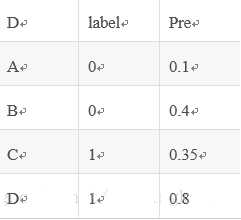
排序。按概率排序后得到：
按照上面的公式，把相关的序号进行一个叠加，然后再去增删查改：
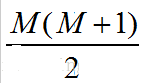
得到：
如果出现得分一样的情况：
假如有4个取值概率为0.5，而且既有正样本也有负样本的情况。计算的时候，其实原则就是相等得分的rank取平均值。具体来说如下：
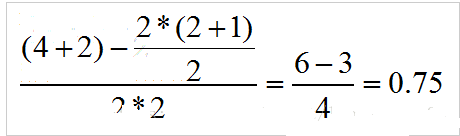
先排序：
这里需要注意的是：相等概率得分的样本，无论正负，谁在前，谁在后无所谓。
由于只考虑正样本的rank值：
对于正样本A，其rank值为7
对于正样本B，其rank值为6
对于正样本E，其rank值为（5+4+3+2）/4
对于正样本F，其rank值为（5+4+3+2）/4
实现及验证
采用sklearn中的库函数验证：
import numpy as np
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
#---自己按照公式实现
def auc_calculate(labels,preds,n_bins=100):
postive_len=sum(labels)
negative_len=len(labels)-postive_len
total_case=postive_len*negative_len
pos_histogram=[0 for _ in range(n_bins)]
neg_histogram=[0 for _ in range(n_bins)]
bin_width=1.0/n_bins
for i in range(len(labels)):
nth_bin=int(preds<i>/bin_width)
if labels<i>==1:
pos_histogram[nth_bin]+=1
else:
neg_histogram[nth_bin]+=1
accumulated_neg=0
satisfied_pair=0
for i in range(n_bins):
satisfied_pair+=(pos_histogram<i>*accumulated_neg+pos_histogram<i>*neg_histogram<i>*0.5)
accumulated_neg+=neg_histogram<i>
return satisfied_pair/float(total_case)
if __name__=='__main__':
y=np.array([1,0,0,0,1,0,1,0,])
pred=np.array([0.9,0.8,0.3,0.1,0.4,0.9,0.66,0.7])
fpr,tpr,thresholds=roc_curve(y,pred,pos_label=1)
print("-----sklearn:",auc(fpr,tpr))
print("-----py脚本:",auc_calculate(y,pred))AUC的优点：
它不受关于平衡性的影响，不同的样本比例，其AUC的评测结果都是一样的。所以我们在训练的时候，可以直接使用AUC作为损失函数。
以上就是小编给大家总结的了，希望可以能给各位读者带来一定的帮助。
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/127815.html
对于很多从事Python的人来说，有很多的人想要去进阶的，比如学习跟多的一些知识，比如，我们在工作中会遇到，使用Python计算AUC的三种方式，下面给大家做出一个解答。 介绍 AUC（Area Under Curve），其实就是ROC曲线围成的和下坐标轴围成的一个面积，这个面积的数值一般是不会大于1的。 当然，ROC曲线基本上都在y=x，这条直线上面的一个正上方，因此AUC的正确值应该...
摘要：问题是什么能拿来干什么如何求解深入理解是什么混淆矩阵混淆矩阵是理解大多数评价指标的基础，毫无疑问也是理解的基础。内容的召回往往是根据的排序而决定的。 问题： AUC是什么 AUC能拿来干什么 AUC如何求解（深入理解AUC） AUC是什么 混淆矩阵(Confusion matrix) 混淆矩阵是理解大多数评价指标的基础，毫无疑问也是理解AUC的基础。丰富的资料介绍着混淆矩阵的概念，...
摘要：问题是什么能拿来干什么如何求解深入理解是什么混淆矩阵混淆矩阵是理解大多数评价指标的基础，毫无疑问也是理解的基础。内容的召回往往是根据的排序而决定的。 问题： AUC是什么 AUC能拿来干什么 AUC如何求解（深入理解AUC） AUC是什么 混淆矩阵(Confusion matrix) 混淆矩阵是理解大多数评价指标的基础，毫无疑问也是理解AUC的基础。丰富的资料介绍着混淆矩阵的概念，...
摘要：精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。分数同时考虑了查准率和查全率，让二者同时达到最高，取一个平衡。接受者操作特征曲线曲线，又称接受 作者：xiaoyu 微信公众号：Python数据科学 知乎：python数据分析师 ROC/AUC作为机器学习的评估指标非常重要，也是面试中经常出现的问题（80%都会问到）。其实，理解它并...
摘要：精准率代表对正样本结果中的预测准确程度，而准确率则代表整体的预测准确程度，既包括正样本，也包括负样本。分数同时考虑了查准率和查全率，让二者同时达到最高，取一个平衡。接受者操作特征曲线曲线，又称接受 作者：xiaoyu 微信公众号：Python数据科学 知乎：python数据分析师 ROC/AUC作为机器学习的评估指标非常重要，也是面试中经常出现的问题（80%都会问到）。其实，理解它并...
阅读 657·2023-01-14 11:38
阅读 484·2023-01-14 11:04
阅读 390·2023-01-14 10:57
阅读 452·2023-01-14 10:48
阅读 500·2023-01-14 10:40
阅读 1300·2023-01-14 10:34
阅读 605·2023-01-14 10:24
阅读 475·2023-01-14 10:18
