什么是树
现实中树随处可见；在计算机世界，树就是一种分层结构的抽象模型。
如下图所示：
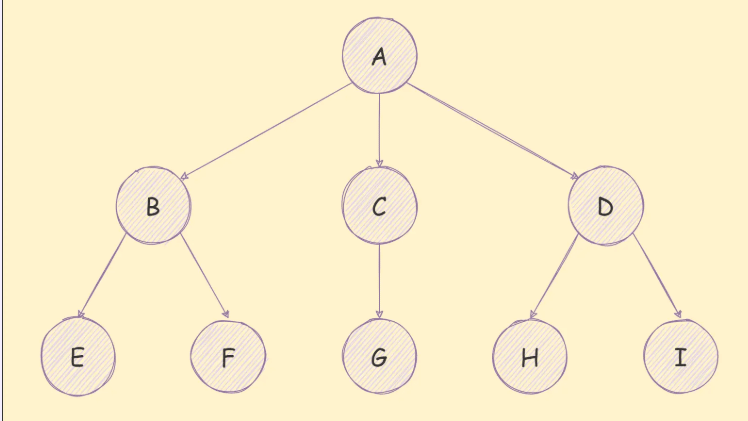
树结构的可以用在很多情景，就如下图公司的组织架构，用“树”就可以表达出来，如下图：
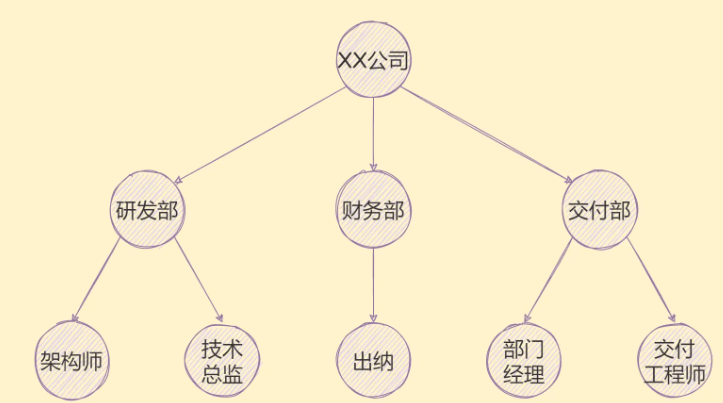
组织架构只是其中之一，比如族谱、省市等用树的结构形式展现是完全可以。
树的术语
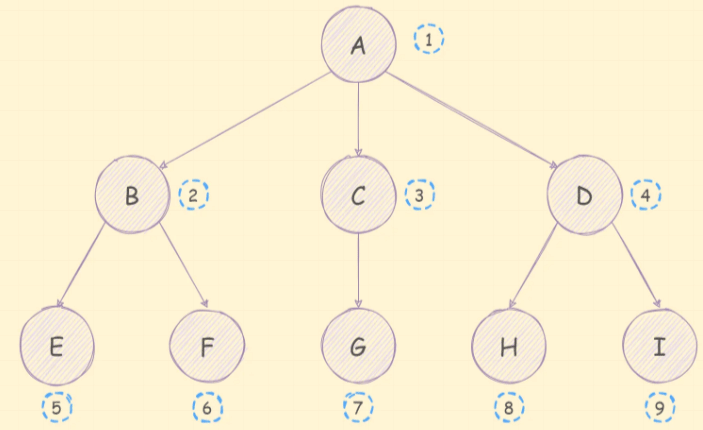
树有很多的术语，如下图：
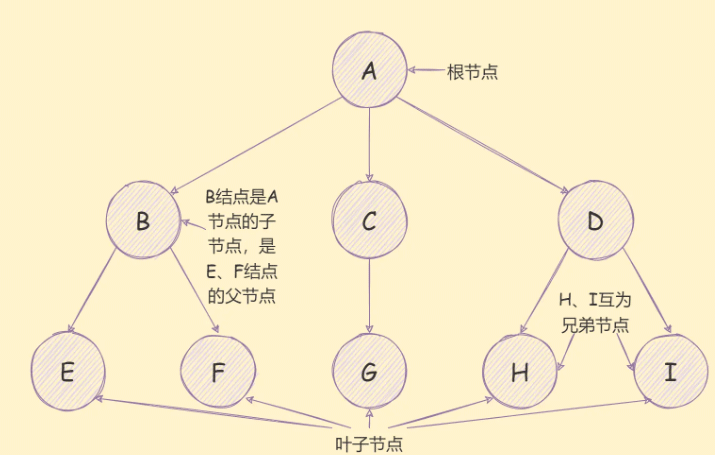
树：n(n≥0)个节点所构成的有限集合，当n=0时，称为空树；
节点的度：节点的子树个数，例如B节点的度就是2，A节点的度就是3；
树的度：树的所有节点中最大的度数，例如上图中，树的度是3；
叶子节点：度为0的节点，也叫叶节点；
子节点：如上图；
兄弟节点：如上图；
根节点：如上图；
树的深度：树中所有结点中的最大层次，例如上图中树的深度就是3；
节点的层次：例如E节点的层次就是3，节点的层次就是父节点层次+1，根节点的层次为1；
路径：一个节点到另一个节点的通道，例如A→H的路径就是A D H；
路径长度：一个节点到另一个节点的距离，例如A→H的路径就是3。
JavaScript中的树
树结构可以作为最常见的数据结构之一，还有很多其他的结构如DOM树、级联选择、树形组件等等；
JavaScript没有这样的结构，开发我们的大脑，想到可以通过对象和数组来模拟一个树，
例如下面这段代码：
const tree = {
value: 'A',
children: [
{
value: 'B',
children: [
{ value: 'E', children: null },
{ value: 'F', children: null },
],
},
{
value: 'C',
children: [{ value: 'G', children: null }],
},
{
value: 'D',
children: [
{ value: 'H', children: null },
{ value: 'I', children: null },
],
},
],
}广度优先和深度优点遍历算法
深度优先
所谓的深度优先遍历算法，就是尽可能深的去搜索树的分支，它的遍历顺序如下图：
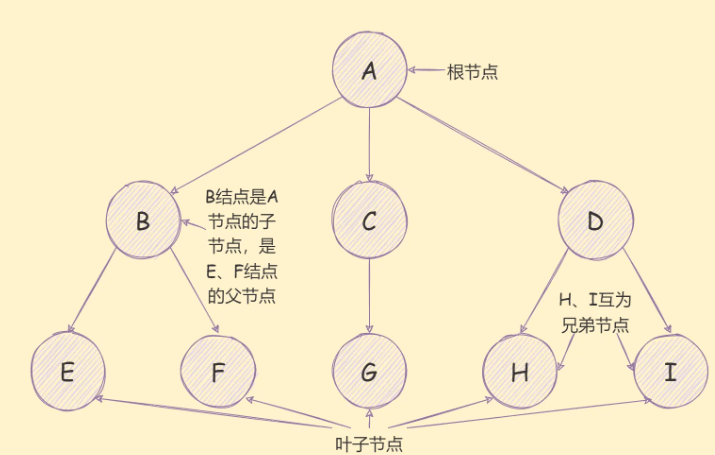
实现思路如下：
访问根节点；
对根节点的children持续进行深度优先遍历（递归）；
实现代码如下：
function dfs(root) {
console.log(root.value)
root.children && root.children.forEach(dfs) // 与下面一致
// if (root.children) {
// root.children.forEach(child => {
// dfs(child)
// })
// }
}
dfs(tree) // 这个tree就是前面定义的那个树
/* 结果
A
B
E
F
C
G
D
H
I
*/上述展示我们想要的表示，思路没什么问题。
广度优先
所谓的广度优先就是依次访问离根节点近的节点，它的遍历顺序如下图：
实现思路如下：
创建要给队列，把根节点入队；
把队头出队并访问；
把队头的children依次入队；
重复执行2、3步，直到队列为空。
实现代码如下：
function bfs(root) {
// 1. 新建队列 跟节点入队
const q = [root]
// 4 重复执行
while (q.length > 0) {
const node = q.shift() // 2 队头出队
console.log(node.value)
// 3 队头 children 依次入队
node.children &&
node.children.forEach(child => {
q.push(child)
})
}
}
bfs(tree)
/* 结果
A
B
C
D
E
F
G
H
I
*/上述展示我们想要的表示，算法没什么问题。
文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。
转载请注明本文地址：https://www.ucloud.cn/yun/127785.html
摘要：通过深度优先遍历两棵树，每层节点进行对比，记录下每个节点的差异。所以可以对那棵树也进行深度优先遍历，遍历的时候从步骤二生成的对象中找出当前遍历的节点差异，然后进行操作。 实现虚拟(Virtual) Dom 把一个div元素的属性打印出来，如下： showImg(https://segmentfault.com/img/bVbnPe1?w=1239&h=336); 可以看到仅仅是第一层，...
摘要：本文所实现的完整代码存放在。这就是所谓的算法。两个树的完全的算法是一个时间复杂度为的问题。如果有差异的话就记录到一个对象里面。如和的不同，会被所替代。这牵涉到两个列表的对比算法，需要另外起一个小节来讨论。 作者：戴嘉华 转载请注明出处并保留原文链接（ https://github.com/livoras/blog/issues/13 ）和作者信息。 目录： 1 前言 2 对前端应用状...
摘要：存在好几种方式来表示这种数据结构。下面的示意图展示了邻接表数据结构。在关联矩阵中矩阵的行表示顶点列表示边。广度优先搜索算法和深度优先搜索算法基本上是相同的只有一点不同那就是待访问顶点列表的数据结构。 1 树 一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点。位于树顶部的节点叫作根节点(11)。它没有父节点。树中的每个元素都叫作...
摘要：算法之深度优先遍历和广度优先遍历背景在开发页面的时候，我们有时候会遇到这种需求在页面某个节点中遍历，找到目标节点，我们正常做法是利用选择器，或者，但在本文，我们从算法的角度去查找节点，同时理解一下深度优先遍历和广度优先遍历的原理。 JS算法之深度优先遍历(DFS)和广度优先遍历(BFS) 背景 在开发页面的时候，我们有时候会遇到这种需求：在页面某个dom节点中遍历，找到目标dom节点，...
阅读 507·2023-03-27 18:33
阅读 710·2023-03-26 17:27
阅读 608·2023-03-26 17:14
阅读 580·2023-03-17 21:13
阅读 505·2023-03-17 08:28
阅读 1757·2023-02-27 22:32
阅读 1265·2023-02-27 22:27
阅读 2107·2023-01-20 08:28
