JavaScript二叉树及各种遍历算法详情

　　在之前的文章中我们有讲过树的相关知识，例如，树的概念、深度优先遍历和广度优先遍历。这篇文章讲述了一个特殊的树——二叉树。

       什么是二叉树

　　二叉树是每个节点最多只能有两个子节点的树，如下图所示：

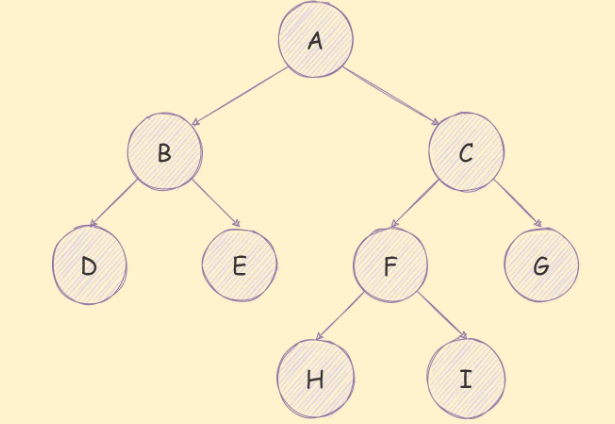
　　一个二叉树具有以下几个特质：

　　要计算在每层有多少个点，可以依据公式2^(i-1)个(i是树的第几层)；

　　如果这颗二叉树的深度为k，那二叉树最多有2^k-1个节点；

　　在一个非空的二叉树中，若使用n0表示叶子节点的个数，n2是度为2的非叶子节点的个数，那么两者满足关系n0 = n2 + 1。

　　满二叉树

　　如果在一个二叉树中，除了叶子节点，其余的节点的每个度都是2，则说明该二叉树是一个满二叉树，

　　如下图所示：

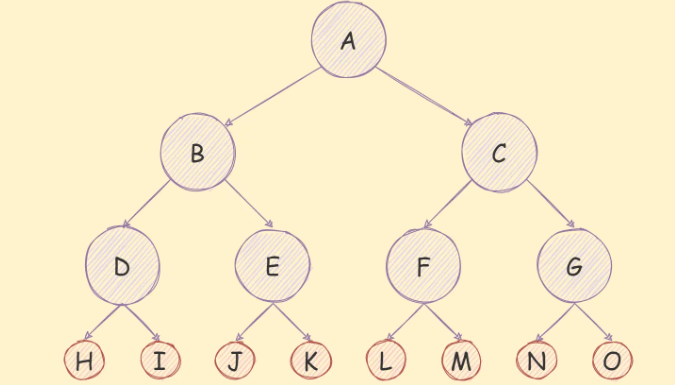
　　满二叉树除了满足普通二叉树特质，还具有如下几个特质：

　　每个层节点公式2^(n-1)（n为层数）；

　　深度为k的满二叉树一定存在2^k-1个节点，叶子节点的个数为2^(k-1)；

　　具有n个节点的满二叉树的深度为log_2^(n+1)。

　　完全二叉树

　　如果一个二叉树去掉最后一次层是满二叉树，且最后一次的节点是依次从左到右分布的，则这个二叉树是一个完全二叉树，

　　如下图所示：

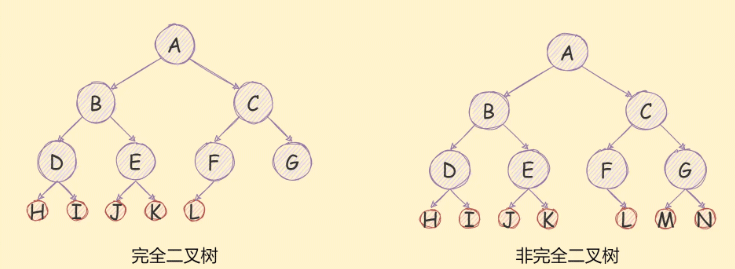
　　二叉树的存储

　　存储二叉树的常见方式分为两种，一种是使用数组存储，另一种使用链表存储。

　　数组存储

　　使用数组存储二叉树，如果遇到完全二叉树，存储顺序从上到下，从左到右，如下图所示：

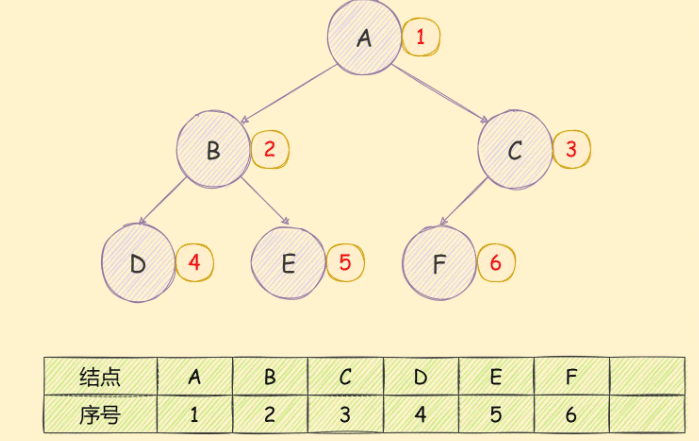
　　如果是一个非完全二叉树，如下图所示：

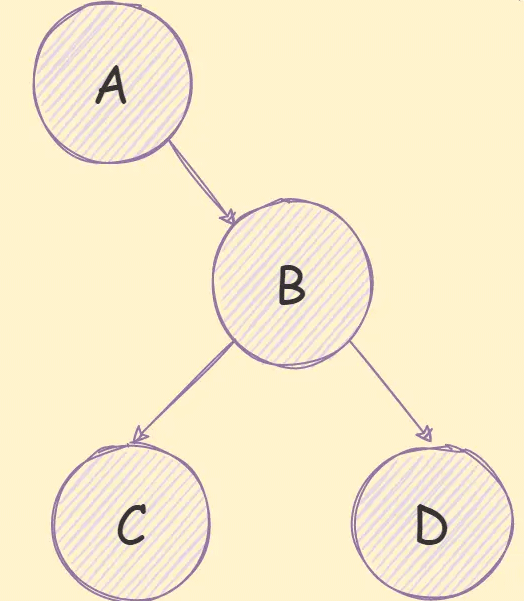
　　需要先将其转换为完全二叉树，然后在进行存储，如下图所示：

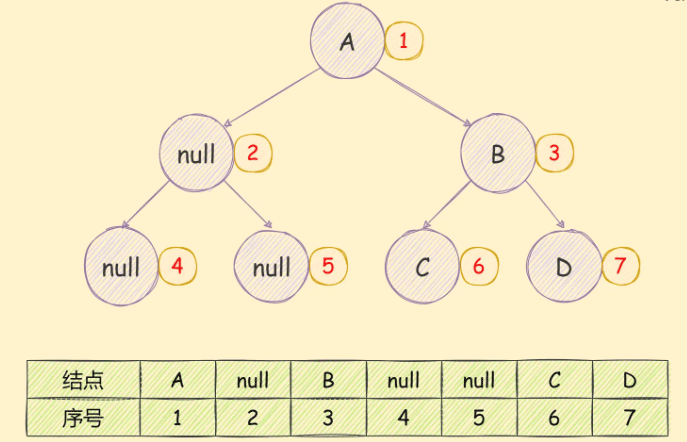
　　可以很明显的看到存储空间的浪费。

　　链表存储

　　使用链表存储通常将二叉树中的分为3个部分，如下图：

　　这三个部分依次是左子树的引用，该节点包含的数据，右子树的引用，存储方式如下图所示：

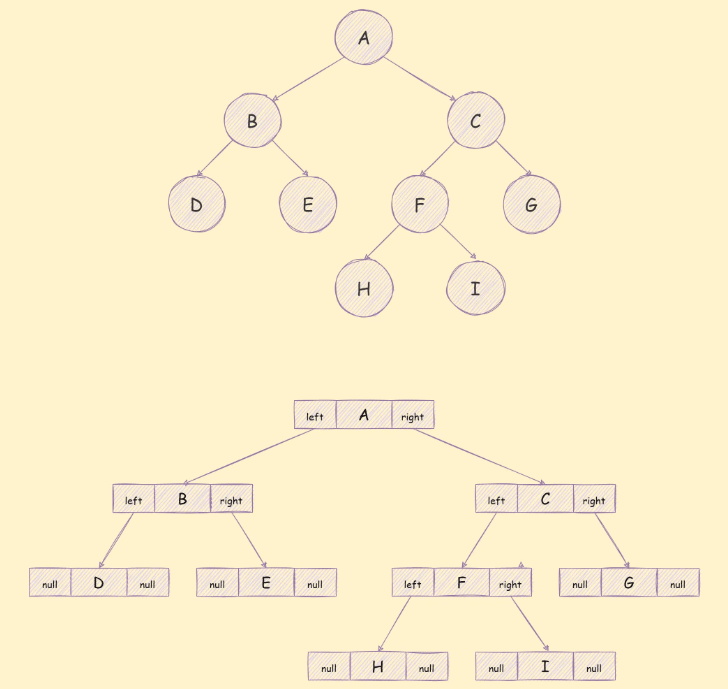
　　与二叉树相关的算法

　　以下算法中遍历用到的树如下：

　　// tree.js
　　const bt = {
　　val: 'A',
　　left: {
　　val: 'B',
　　left: { val: 'D', left: null, right: null },
　　right: { val: 'E', left: null, right: null },
　　},
　　right: {
　　val: 'C',
　　left: {
　　val: 'F',
　　left: { val: 'H', left: null, right: null },
　　right: { val: 'I', left: null, right: null },
　　},
　　right: { val: 'G', left: null, right: null },
　　},
　　}
　　module.exports = bt

　　深度优先遍历

　　二叉树的深度优先遍历与树的深度优先遍历思路一致，思路如下：

　　访问根节点；

　　访问根节点的left

　　访问根节点的right

　　重复执行第二三步

　　实现代码如下：

　　const bt = {
　　val: 'A',
　　left: {
　　val: 'B',
　　left: { val: 'D', left: null, right: null },
　　right: { val: 'E', left: null, right: null },
　　},
　　right: {
　　val: 'C',
　　left: {
　　val: 'F',
　　left: { val: 'H', left: null, right: null },
　　right: { val: 'I', left: null, right: null },
　　},
　　right: { val: 'G', left: null, right: null },
　　},
　　}
　　function dfs(root) {
　　if (!root) return
　　console.log(root.val)
　　root.left && dfs(root.left)
　　root.right && dfs(root.right)
　　}
　　dfs(bt)
　　/** 结果
　　A B D E C F H I G
　　*/

　　广度优先遍历

　　实现思路如下：

　　创建队列，把根节点入队

　　把对头出队并访问

　　把队头的left和right依次入队

　　重复执行2、3步，直到队列为空

　　实现代码如下：

　　function bfs(root) {
　　if (!root) return
　　const queue = [root]
　　while (queue.length) {
　　const node = queue.shift()
　　console.log(node.val)
　　node.left && queue.push(node.left)
　　node.right && queue.push(node.right)
　　}
　　}
　　bfs(bt)
　　/** 结果
　　A B C D E F G H I
　　*/

　　先序遍历

　　二叉树的先序遍历实现思想如下：

　　访问根节点;

　　对当前节点的左子树进行先序遍历；

　　对当前节点的右子树进行先序遍历；

　　如下图所示：

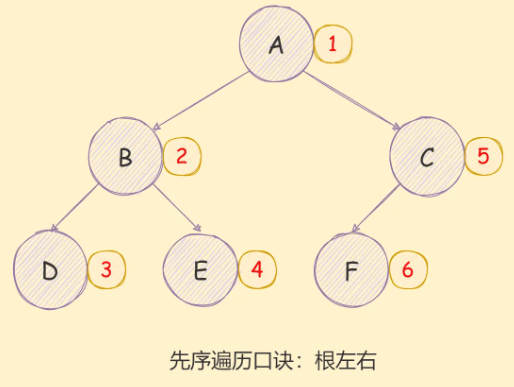
　　递归方式实现如下：

　　const bt = require('./tree')
　　function preorder(root) {
　　if (!root) return
　　console.log(root.val)
　　preorder(root.left)
　　preorder(root.right)
　　}
　　preorder(bt)
　　/** 结果
　　A B D E C F H I G
　　*/

　　迭代方式实现如下：

　　// 非递归版
　　function preorder(root) {
　　if (!root) return
　　// 定义一个栈，用于存储数据
　　const stack = [root]
　　while (stack.length) {
　　const node = stack.pop()
　　console.log(node.val)
　　/* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
　　node.right && stack.push(node.right)
　　node.left && stack.push(node.left)
　　}
　　}
　　preorder(bt)
　　/** 结果
　　A B D E C F H I G
　　*/

　　中序遍历

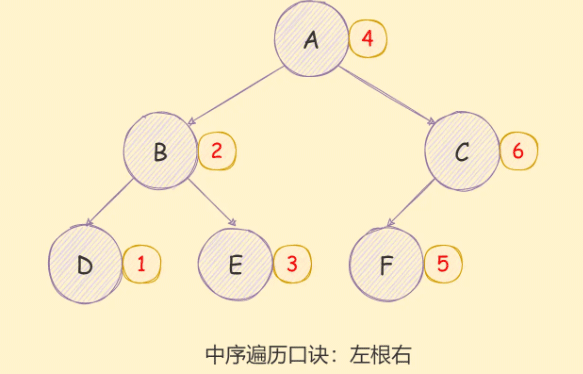
　　二叉树的中序遍历实现思想如下：

　　对当前节点的左子树进行中序遍历；

　　访问根节点;

　　对当前节点的右子树进行中序遍历；

　　如下图所示：

　　递归方式实现如下：

　　const bt = require('./tree')
　　// 递归版
　　function inorder(root) {
　　if (!root) return
　　inorder(root.left)
　　console.log(root.val)
　　inorder(root.right)
　　}
　　inorder(bt)
　　/** 结果
　　D B E A H F I C G
　　*/

　　迭代方式实现如下：

　　// 非递归版
　　function inorder(root) {
　　if (!root) return
　　const stack = []
　　// 定义一个指针
　　let p = root
　　// 如果栈中有数据或者p不是null，则继续遍历
　　while (stack.length || p) {
　　// 如果p存在则一致将p入栈并移动指针
　　while (p) {
　　// 将 p 入栈，并以移动指针
　　stack.push(p)
　　p = p.left
　　}
　　const node = stack.pop()
　　console.log(node.val)
　　p = node.right
　　}
　　}
　　inorder(bt)
　　/** 结果
　　D B E A H F I C G
　　*/

　　后序遍历

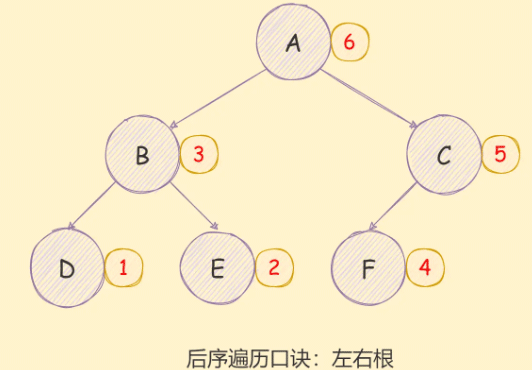
　　二叉树的后序遍历实现思想如下：

　　对当前节点的左子树进行后序遍历；

　　对当前节点的右子树进行后序遍历；

　　访问根节点;

　　如下图所示：

　　递归方式实现如下：　

　const bt = require('./tree')
　　// 递归版
　　function postorder(root) {
　　if (!root) return
　　postorder(root.left)
　　postorder(root.right)
　　console.log(root.val)
　　}
　　postorder(bt)
　　/** 结果
　　D E B H I F G C A
　　*/

　　迭代方式实现如下：

　　// 非递归版
　　function postorder(root) {
　　if (!root) return
　　const outputStack = []
　　const stack = [root]
　　while (stack.length) {
　　const node = stack.pop()
　　outputStack.push(node)
　　// 这里先入left需要保证left后出，在stack中后出，就是在outputStack栈中先出
　　node.left && stack.push(node.left)
　　node.right && stack.push(node.right)
　　}
　　while (outputStack.length) {
　　const node = outputStack.pop()
　　console.log(node.val)
　　}
　　}
　　postorder(bt)
　　/** 结果
　　D E B H I F G C A
　　*/

　　关于二叉树及各种遍历算法相关内容已讲述完毕。