JavaScript二叉搜索树构建操作详解

　　今天我们一起学习什特殊的二叉树二叉搜索树（BSTBinary Search Tree），您也可以叫它二叉排序树、二叉查找树。现在我们看看。

      二叉搜索树说说明

　　二叉搜索树顾名思义就是树形叉一样，现在说特质：

　　对于任何一个非空节点来说，它左子树上的值必须小于当前值；

　　对于任何一个非空节点来说，它右子树上的值必须大于当前值；

　　任何一颗子树满足上面的条件；

　　如下图所示：

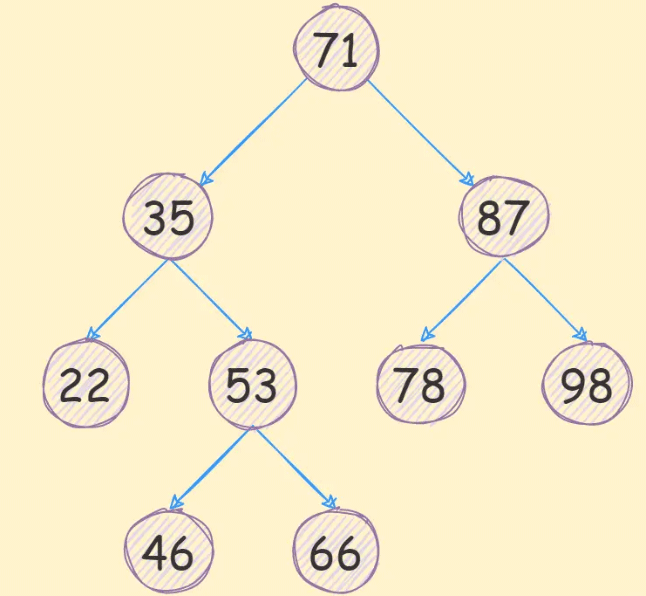
　　上图就是一颗二叉搜索树，总结来说就是右边数值大于左边数值。上图的根节点的值71，它的左子树的值分别是22、35、46、53和66，这几个都是满足左子树小于当前值；它的右子树的值分别是78、87和98，这几个值是满足右子树大于当前值的；上述就显示出二叉搜索树特质。

　　根据二叉搜索树的特质，我们还能得到以下结论：

　　二叉搜索树的任何一个节点的左子树、右子树都是一颗二叉搜索树；

　　二叉搜索树的最小的节点是整颗树的最左下角的叶子节点；

　　二叉搜索树的最大的节点是整棵树的最右下角的叶子节点；

　　构建一颗二叉搜索树

　　先项目中用avaScript来实现构建一颗二叉搜索树，我们可以想象成一个一个节点组成，这里我们就用于class创建一个节点类，

　　示例代码如下：

　　class BinarySearchTree {
　　constructor() {
　　// 初始化根节点
　　this.root = null
　　}
　　// 创建一个节点
　　Node(val) {
　　return {
　　left: null, // 左子树
　　right: null, // 右子树
　　parent: null, // 父节点
　　val,
　　}
　　}
　　}

　　这里一个节点由四部分组成，分别是指向左子树的指针、指向右子树的指针、指向父节点的指针以及当前值。

　　二叉搜索树的操作

　　关于二叉树的遍历操作我们在上一篇文章中已经介绍了，这里不在重复，这里主要介绍如下操作：

　　插入操作

　　查找操作

　　删除操作

　　向二叉搜索树中插入数据

　　向一个二叉搜索树插入数据实现思路如下：

　　判断root是否为空，如果为空则创建root；

　　如果root非空，则需要判断插入节点的val比根节点的val是大还是小；

　　如果比根节点小，说明是左子树的节点；

　　如果比根节点大，说明是右子树的节点；

　　上面重复执行直至我们找到一个点，当这个点小于我们要插入的值，且不存在右子树，将这个点作为其右叶子节点；当这个点大于我们要插入的值，且不存在右子树，将这个点作为其左叶子节点。

　　示例代码如下

　　// 创建要给插入节点的方法
　　insertNode(val) {
　　const that = this
　　// 允许接受一个数组，批量插入
　　if (Object.prototype.toString.call(val) === '[object Array]') {
　　val.forEach(function (v) {
　　that.insertNode(v)
　　})
　　return
　　}
　　if (typeof val !== 'number') throw Error('插入的值不是一个数字')
　　const newNode = this.Node(val)
　　if (this.root) {
　　// 根节点非空
　　this.#insertNode(this.root, newNode)
　　} else {
　　// 根节点是空的，直接创建
　　this.root = newNode
　　}
　　}
　　// 私有方法，插入节点
　　#insertNode(root, newNode) {
　　if (newNode.val < root.val) {
　　// 新节点比根节点小，左子树
　　if (root.left === null) {
　　// 如果左子树上没有内容，则直接插入，如果有，寻找下一个插入位置
　　root.left = newNode
　　root.left.parent = root
　　} else {
　　this.#insertNode(root.left, newNode)
　　}
　　} else {
　　// 新节点比根节点大，右子树
　　if (root.right === null) {
　　// 如果右子树上没有内容，则直接插入，如果有，寻找下一个插入位置
　　root.right = newNode
　　root.right.parent = root
　　} else {
　　this.#insertNode(root.right, newNode)
　　}
　　}
　　}

　　在类中定义了insertNode方法，这个方法接受数值或者数值类型的数组，将其插入这个二叉搜索树中；插入方法我们定义了一个私有的#insertNode方法，用于节点的插入。

　　现在为实现预估动作结果，在这里定义了一个静态方法，用于中序遍历（因为中序遍历的顺序是左根右，在二叉搜索树中使用中序排序，最终结果是从小到大依次排序的）这个树，并返回一个数组，

　　示例代码如下：

　　// 中序遍历这个树
　　static inorder(root) {
　　if (!root) return
　　const result = []
　　const stack = []
　　// 定义一个指针
　　let p = root
　　// 如果栈中有数据或者p不是null，则继续遍历
　　while (stack.length || p) {
　　// 如果p存在则一致将p入栈并移动指针
　　while (p) {
　　// 将 p 入栈，并以移动指针
　　stack.push(p)
　　p = p.left
　　}
　　const node = stack.pop()
　　result.push(node.val)
　　p = node.right
　　}
　　return result
　　}

　　测试代码如下：

　　const tree = new BinarySearchTree()

　　tree.insertNode([71, 35, 87, 22, 53, 46, 66, 78, 98])

　　const arr = BinarySearchTree.inorder(tree.root)

　　console.log(arr) // [ 22, 35, 46, 53, 66,71, 78, 87, 98 ]

　　最终的树结构如下：

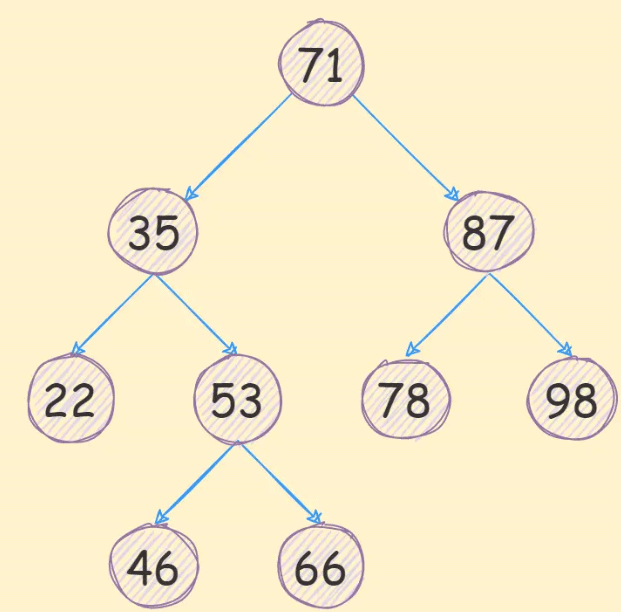
　　查找二叉搜索树中的数据

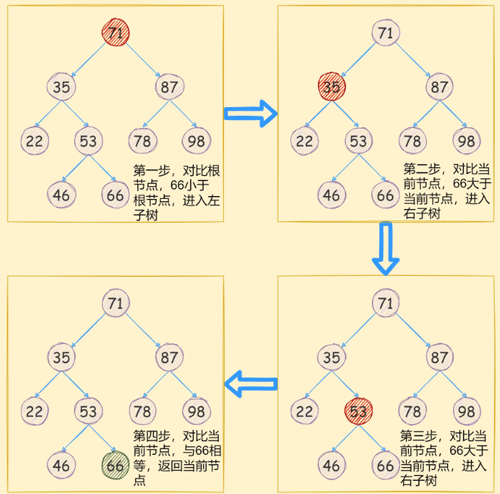
　　现在我们封装一个find方法，用于查找二叉搜索树中的某个数据，假如我们查找66这个数据，利用上面那个树，

　　其查找思路如下图所示：

　　递归方式实现如下：

　　/**
　　* 根据 val 查找节点
　　* @param {number} val 需要查找的数值
　　* @returns 如果找到返回当前节点的引用，如果未找到返回 undefined
　　*/
　　find(val) {
　　if (typeof val !== 'number') throw Error('插入的值不是一个数字')
　　let node = this.root
　　while (node) {
　　if (node.val < val) {
　　// 进入右子树
　　node = node.right
　　} else if (node.val > val) {
　　// 进入左子树
　　node = node.left
　　} else {
　　return node
　　}
　　}
　　return
　　}

　　两者相对来说，使用迭代的方式更优一些。

　　删除二叉搜索树的某个节点

　　前驱后继节点

　　在开始删除二叉搜索树中的某个节点之前，我们先来了解一下什么是前驱和后继节点；

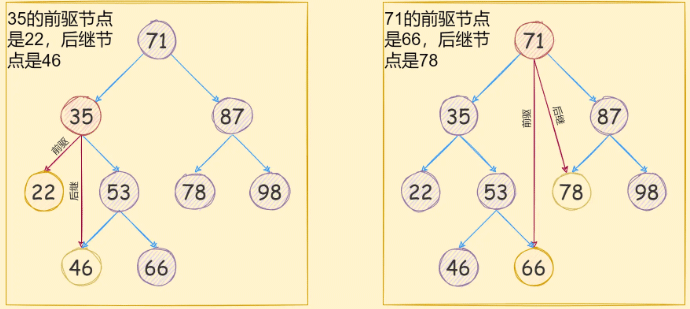
　　前驱节点指的是使用中序遍历当前二叉搜索树时，当前节点的上一个节点就是前驱节点，换一种说法就是在二叉搜索树中，当前节点的左子树的最大值，就是该节点的前驱节点；

　　后继节点指的是使用中序遍历当前二叉搜索树时，当前节点的下一个节点就是后继节点，换一种说法就是在二叉搜索树中，当前节点的右子树的最小值，就是该节点的后继节点；

　　如下图所示：

　　了解了什么是前驱和后继节点之后，现在我们来开始删除某个节点。

　　删除一个节点的三种情况

　　当删除的节点是叶子节点时，只需要将指向它的指针修改为null，即可，如下图所示：

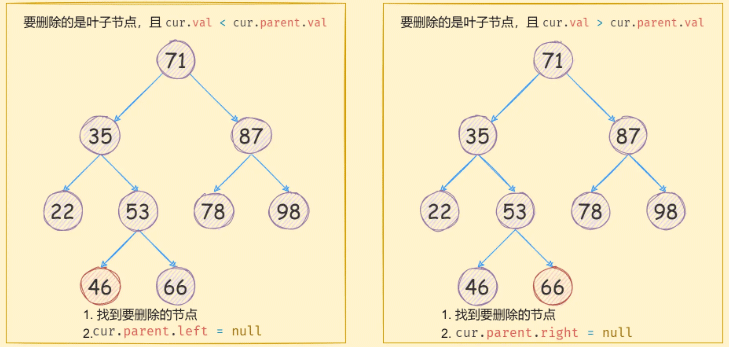
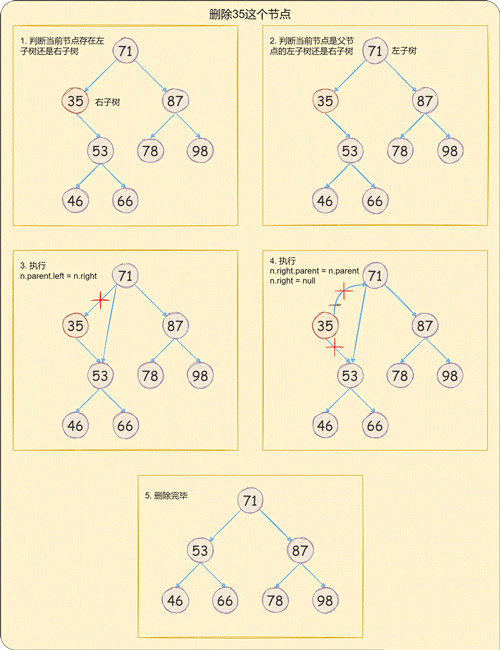
　　当需要删除的节点存在一个子节点时，需要将要删除节点的子节点的parent指针指向要删除节点的父节点，然后将当前要删除节点的父节点指向子节点即可，

　　如下图所示：

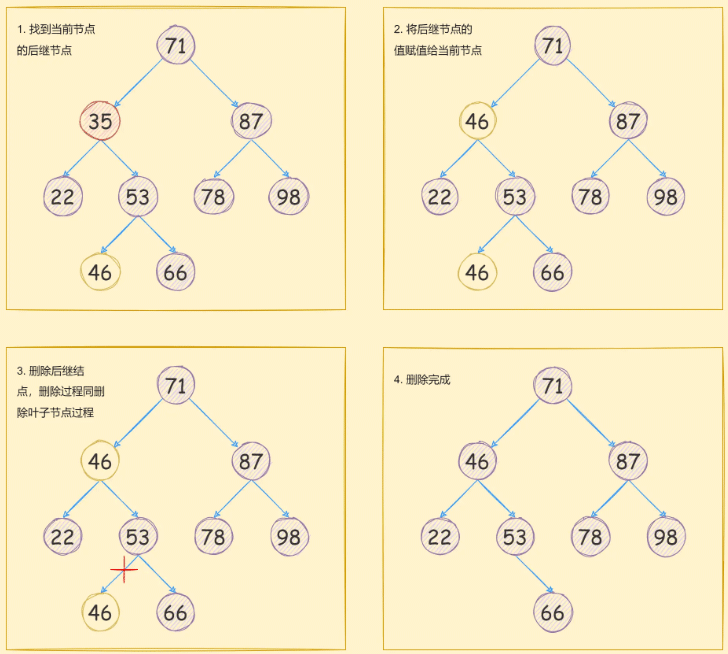
　　当需要删除的节点存在一个子节点时， 删除步骤如下：

　　找到当前节点的前驱或者后继节点，这里选择后继；

　　然后将后继节点的值赋值给当前节点；

　　删除后继节点。

　　如下图所示：

　　现在我们将这些情况已经分析完成了，现在通过代码实现一下。

　　实现代码

　　实现代码如下：

　　remove(val) {
　　// 1. 删除节点
　　const cur = this.find(val)
　　if (!val) return false // 未找到需要删除的节点
　　if (!cur.left && !cur.right) {
　　// 1. 当前节点是叶子节点的情况
　　this.#removeLeaf(cur)
　　} else if (cur.left && cur.right) {
　　// 2. 当前节点存在两个子节点
　　// 2.1 找到当前节点的后继节点
　　const successorNode = this.#minNode(cur.right)
　　// 2.2 将后继节点的值赋值给当前值
　　cur.val = successorNode.val
　　if (!successorNode.left && !successorNode.right) {
　　// 2.3 后继节点是叶子节点，直接删除
　　this.#removeLeaf(successorNode)
　　} else {
　　// 2.4 后继节点不是叶子节点
　　// 2.4.1记录该节点的子节点，
　　let child =
　　successorNode.left !== null ? successorNode.left : successorNode.right
　　// 2.4.2 记录该节点的父节点
　　let parent = successorNode.parent
　　// 2.4.3 如果当前父节点的left是后继结点，则把后继结点的父节点的left指向后继结点的子节点
　　if (parent.left === successorNode) {
　　parent.left = child
　　} else {
　　// 2.4.4 如果不是，则让父节点的right指向后继结点的子节点
　　parent.right = child
　　}
　　// 2.4.5 修改子节点的parent指针
　　child.parent = parent
　　}
　　// 2.3 删除后继节点
　　} else {
　　// 记录当前节点的是否是父节点的左子树
　　const isLeft = cur.val < cur.parent.val
　　// 3. 仅存在一个子节点
　　if (cur.left) {
　　// 3.1 当前节点存在左子树
　　cur.parent[isLeft ? 'left' : 'right'] = cur.left
　　cur.left.parent = cur.parent
　　} else if (cur.right) {
　　// 3.2 当前节点存在右子树
　　cur.parent[isLeft ? 'left' : 'right'] = cur.right
　　cur.right.parent = cur.parent
　　}
　　}
　　}
　　// 删除叶子节点
　　#removeLeaf(node) {
　　if (!node) return
　　const parent = node.parent
　　if (node.val < parent.val) {
　　// 当前要删除的叶子节点是左节点
　　parent.left = null
　　} else {
　　// 当前要删除的叶子节点是右节点
　　parent.right = null
　　}
　　}
　　// 查找最小值
　　#minNode(node) {
　　if (!node) return
　　if (!node.left) return node
　　let p = node.left
　　while (p.left) {
　　p = p.left
　　}
　　return p
　　}

　　完整代码

　　本篇文章中的完整代码如下：

　　class BinarySearchTree {
　　constructor() {
　　// 初始化根节点
　　this.root = null
　　}
　　// 创建一个节点
　　Node(val) {
　　return {
　　left: null, // 左子树
　　right: null, // 右子树
　　parent: null, // 父节点
　　val,
　　}
　　}
　　/**
　　* 创建要给插入节点的方法
　　* @param {number | array[number]} val
　　* @returns
　　*/
　　insertNode(val) {
　　const that = this
　　// 允许接受一个数组，批量插入
　　if (Object.prototype.toString.call(val) === '[object Array]') {
　　val.forEach(function (v) {
　　that.insertNode(v)
　　})
　　return
　　}
　　if (typeof val !== 'number') throw Error('插入的值不是一个数字')
　　const newNode = this.Node(val)
　　if (this.root) {
　　// 根节点非空
　　this.#insertNode(this.root, newNode)
　　} else {
　　// 根节点是空的，直接创建
　　this.root = newNode
　　}
　　}
　　/**
　　* 私有方法，插入节点
　　* @param {Object{Node}} root
　　* @param {Object{Node}} newNode
　　*/
　　#insertNode(root, newNode) {
　　if (newNode.val < root.val) {
　　// 新节点比根节点小，左子树
　　if (root.left === null) {
　　// 如果左子树上没有内容，则直接插入，如果有，寻找下一个插入位置
　　root.left = newNode
　　root.left.parent = root
　　} else {
　　this.#insertNode(root.left, newNode)
　　}
　　} else {
　　// 新节点比根节点大，右子树
　　if (root.right === null) {
　　root.right = newNode
　　root.right.parent = root
　　} else {
　　this.#insertNode(root.right, newNode)
　　}
　　}
　　}
　　/**
　　* 根据 val 查找节点
　　* @param {number} val 需要查找的数值
　　* @returns 如果找到返回当前节点的引用，如果未找到返回 undefined
　　*/
　　find(val) {
　　if (typeof val !== 'number') throw Error('插入的值不是一个数字')
　　let node = this.root
　　while (node) {
　　if (node.val < val) {
　　// 进入右子树
　　node = node.right
　　} else if (node.val > val) {
　　// 进入左子树
　　node = node.left
　　} else {
　　return node
　　}
　　}
　　return
　　}
　　// /**
　　// * 根据 val 查找节点 递归版
　　// * @param {number} val 需要查找的数值
　　// * @returns 如果找到返回当前节点的引用，如果未找到返回 undefined
　　// */
　　// find(val) {
　　// if (typeof val !== 'number') throw Error('插入的值不是一个数字')
　　// function r(node, val) {
　　// // console.log(node)
　　// if (!node) return
　　// if (node.val < val) {
　　// return r(node.right, val)
　　// } else if (node.val > val) {
　　// return r(node.left, val)
　　// } else {
　　// return node
　　// }
　　// }
　　// return r(this.root, val)
　　// }
　　remove(val) {
　　// 1. 删除节点
　　const cur = this.find(val)
　　if (!val) return false // 未找到需要删除的节点
　　if (!cur.left && !cur.right) {
　　// 1. 当前节点是叶子节点的情况
　　this.#removeLeaf(cur)
　　} else if (cur.left && cur.right) {
　　// 2. 当前节点存在两个子节点
　　// 2.1 找到当前节点的后继节点
　　const successorNode = this.#minNode(cur.right)
　　// 2.2 将后继节点的值赋值给当前值
　　cur.val = successorNode.val
　　if (!successorNode.left && !successorNode.right) {
　　// 2.3 后继节点是叶子节点，直接删除
　　this.#removeLeaf(successorNode)
　　} else {
　　// 2.4 后继节点不是叶子节点
　　// 2.4.1记录该节点的子节点，
　　let child =
　　successorNode.left !== null ? successorNode.left : successorNode.right
　　// 2.4.2 记录该节点的父节点
　　let parent = successorNode.parent
　　// 2.4.3 如果当前父节点的left是后继结点，则把后继结点的父节点的left指向后继结点的子节点
　　if (parent.left === successorNode) {
　　parent.left = child
　　} else {
　　// 2.4.4 如果不是，则让父节点的right指向后继结点的子节点
　　parent.right = child
　　}
　　// 2.4.5 修改子节点的parent指针
　　child.parent = parent
　　}
　　// 2.3 删除后继节点
　　} else {
　　// 记录当前节点的是否是父节点的左子树
　　const isLeft = cur.val < cur.parent.val
　　// 3. 仅存在一个子节点
　　if (cur.left) {
　　// 3.1 当前节点存在左子树
　　cur.parent[isLeft ? 'left' : 'right'] = cur.left
　　cur.left.parent = cur.parent
　　} else if (cur.right) {
　　// 3.2 当前节点存在右子树
　　cur.parent[isLeft ? 'left' : 'right'] = cur.right
　　cur.right.parent = cur.parent
　　}
　　}
　　}
　　// 删除叶子节点
　　#removeLeaf(node) {
　　if (!node) return
　　const parent = node.parent
　　if (node.val < parent.val) {
　　// 当前要删除的叶子节点是左节点
　　parent.left = null
　　} else {
　　// 当前要删除的叶子节点是右节点
　　parent.right = null
　　}
　　}
　　// 查找最小值
　　#minNode(node) {
　　if (!node) return
　　if (!node.left) return node
　　let p = node.left
　　while (p.left) {
　　p = p.left
　　}
　　return p
　　}
　　// 中序遍历这个树
　　static inorder(root) {
　　if (!root) return
　　const result = []
　　const stack = []
　　// 定义一个指针
　　let p = root
　　// 如果栈中有数据或者p不是null，则继续遍历
　　while (stack.length || p) {
　　// 如果p存在则一致将p入栈并移动指针
　　while (p) {
　　// 将 p 入栈，并以移动指针
　　stack.push(p)
　　p = p.left
　　}
　　const node = stack.pop()
　　result.push(node.val)
　　p = node.right
　　}
　　return result
　　}
　　}
　　const tree = new BinarySearchTree()
　　tree.insertNode([71, 35, 84, 22, 53, 46, 66, 81, 83, 82, 88, 98])
　　console.log(BinarySearchTree.inorder(tree.root)) // [ 22, 35, 46, 53, 66, 71, 81, 82, 83, 84, 88, 98 ]
　　tree.remove(71
　　console.log(BinarySearchTree.inorder(tree.root)) // [ 22, 35, 46, 53, 66, 81, 82, 83, 84, 88, 98 ]

　　总结

　　此篇结束，大家可以更多深入了解关于二叉搜索树的其他内容。