怎么利用Python和C语言实现哈夫曼编码（霍夫曼编码）

89542767 发布于2022-09-09 09:53 / 752人阅读

　　小编写这篇文章的主要目的是，教给大家怎么使用哈夫曼编码，也就是霍夫曼编码，并把具体的一些代码实例给大家贴了出来，希望可以为大家带来帮助。

　　一、用C语言实现哈夫曼编码

　　1、代码解释

　　（1）建立一个互相连接的表

　　我们在创建哈夫曼树的过程之中，要对互相之间的连接点进行增删查改，所以使用双向链路表格会更加的容易。

'''C
#include <stdlib.h>
#include <stdio.h>
#include <windows.h>
 
 
//哈夫曼树结构体，数据域存储字符及其权重
typedef struct node
{
    char c;
    int weight;
    struct node *lchild, *rchild;
}Huffman, *Tree;
 
 
//双向链表结构体，数据域存储哈夫曼树结点
typedef struct list
{
    Tree root;
    struct list *pre;
    struct list *next;
}List, *pList;
 
 
//创建双向链表，返回头结点指针
pList creatList()
{
    pList head = (pList)malloc(sizeof(List));
 
    pList temp1 = head;
    pList temp2 = (pList)malloc(sizeof(List));
    temp1->pre = NULL;
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'a';
    temp1->root->weight = 22;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
    
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp2 = (pList)malloc(sizeof(List));
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'b';
    temp1->root->weight = 5;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
    
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp2 = (pList)malloc(sizeof(List));
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'c';
    temp1->root->weight = 38;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp2 = (pList)malloc(sizeof(List));
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'd';
    temp1->root->weight = 9;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp2 = (pList)malloc(sizeof(List));
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'e';
    temp1->root->weight = 44;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp2 = (pList)malloc(sizeof(List));
    temp1->next = temp2;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'f';
    temp1->root->weight = 12;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
 
    temp2->pre = temp1;
    temp1 = temp2;
    temp1->next = NULL;
    temp1->root = (Tree)malloc(sizeof(Huffman));
    temp1->root->c = 'g';
    temp1->root->weight = 65;
    temp1->root->lchild = NULL;
    temp1->root->rchild = NULL;
 
    return head;                          
}

　　（2）建立起栈的结构

　　解码过程需要用到两个栈，一个用来存放树结点，一个用来存放码0和1

'''C
#define STACK_INIT_SIZE 100   //栈初始开辟空间大小
#define STACK_INCREMENT 10    //栈追加空间大小
 
//字符栈结构体，存放编码'0'和'1'
typedef struct {
    char *base;
    char *top;
    int size;
}charStack;
 
 
//栈初始化
charStack charStackInit()
{
    charStack s;
    s.base = (char *)malloc(sizeof(char)*STACK_INIT_SIZE);
    s.top = s.base;
    s.size = STACK_INIT_SIZE;
    return s;
}
 
//入栈
void charPush(charStack *s, char e)
{
    if(s->top - s->base >= s->size)
    {
        s->size += STACK_INCREMENT;
        s->base = realloc(s->base, sizeof(char)*s->size);
    }
    *s->top = e;
    s->top++;
}
 
//出栈
char charPop(charStack *s)
{
    if(s->top != s->base)
    {
        s->top--;
        return *s->top;
    }
    return -1;
}
 
//得到栈顶元素，但不出栈
char charGetTop(charStack *s)
{
    s->top--;
    char temp = *s->top;
    s->top++;
    return temp;
}
 
//栈结构体，存放哈夫曼树结点
typedef struct 
{
    Huffman *base;
    Huffman *top;
    int size;
}BiStack;
 
//栈初始化
BiStack stackInit()
{
    BiStack s;
    s.base = (Huffman *)malloc(sizeof(Huffman)*STACK_INIT_SIZE);
    s.top = s.base;
    s.size =STACK_INIT_SIZE;
    return s;
}
 
//入栈
void push(BiStack *s, Huffman e)
{
    if(s->top - s->base >= s->size)
    {
        s->size += STACK_INCREMENT;
        s->base = (Huffman *)realloc(s->base, sizeof(Huffman)*s->size);
    }
    *s->top = e;
    s->top++;
}
 
//出栈
Huffman pop(BiStack *s)
{
    Huffman temp;
    s->top--;
    temp = *s->top;
    return temp;
}
 
//得到栈顶元素，但不出栈
Huffman getTop(BiStack s)
{
    Huffman temp;
    s.top--;
    temp = *s.top;
    return temp;
}
 
char stack[7][10];             //记录a~g的编码
//遍历栈，得到字符c的编码
void traverseStack(charStack s, char c)
{
    int index = c - 'a'; 
    int i = 0;
    while(s.base != s.top)
    {
        stack[index][i] = *s.base;
        i++;
        s.base++;
    }
}

　　（3）创建哈夫曼树

'''C
//通过双向链表创建哈夫曼树，返回根结点指针
Tree creatHuffman(pList head)
{
    pList list1 = NULL;
    pList list2 = NULL;
    pList index = NULL;
    Tree root = NULL;
    while(head->next != NULL)   //链表只剩一个结点时循环结束，此结点数据域即为哈夫曼树的根结点
    {
        list1 = head;
        list2 = head->next;
        index = list2->next;
        root = (Tree)malloc(sizeof(Huffman));
        while(index != NULL)    //找到链表中权重最小的两个结点list1,list2
        {
            if(list1->root->weight > index->root->weight || list2->root->weight > index->root->weight)
            {
                if(list1->root->weight > list2->root->weight) list1 = index;
                else list2 = index;
            }
            index = index->next;
        }
        //list1和list2设为新结点的左右孩子
        if(list2->root->weight > list1->root->weight)
        {
            root->lchild = list1->root;
            root->rchild = list2->root;
        }
        else
        {
            root->lchild = list2->root;
            root->rchild = list1->root;
        }
        //新结点字符统一设为空格，权重设为list1与list2权重之和
        root->c = ' ';
        root->weight = list1->root->weight + list2->root->weight;
        //list1数据域替换成新结点，并删除list2
        list1->root = root;
        list2->pre->next = list2->next;
        if(list2->next != NULL)
            list2->next->pre = list2->pre;    
    }
    return head->root;
}

　　（4）编码

'''C
char stack[7][10];             //记录a~g的编码
//遍历栈，得到字符c的编码
void traverseStack(charStack s, char c)
{
    int index = c - 'a'; 
    int i = 0;
    while(s.base != s.top)
    {
        stack[index][i] = *s.base;
        i++;
        s.base++;
    }
}
 
 
//通过哈夫曼树编码
void encodeHuffman(Tree T)
{  
    BiStack bs = stackInit();
    charStack cs = charStackInit();
    Huffman root = *T;  
    Tree temp = NULL;
    push(&bs, root);      //根结点入栈
    while(bs.top != bs.base)      //栈空表示遍历结束
    {
        root = getTop(bs);
        temp = root.lchild;       //先访问左孩子
        while(temp != NULL)       //左孩子不为空
        {
            //将结点左孩子设为空，代表已访问其左孩子
            root.lchild = NULL;
            pop(&bs);            
            push(&bs, root);
            //左孩子入栈
            root = *temp;
            temp = root.lchild;
            push(&bs, root);
            //'0'入字符栈
            charPush(&cs, '0');
        }
        temp = root.rchild;     //后访问右孩子     
        while(temp == NULL)     //右孩子为空，代表左右孩子均已访问，结点可以出栈 
        {
            //结点出栈
            root = pop(&bs);
            //寻到叶子结点，可以得到结点中字符的编码
            if(root.c != ' ')
                traverseStack(cs, root.c);
            charPop(&cs);       //字符栈出栈
            if(bs.top == bs.base) break;    //根结点出栈，遍历结束
            //查看上一级结点是否访问完左右孩子  
            root = getTop(bs);
            temp = root.rchild;           
        }
        if(bs.top != bs.base)
        {
            //将结点右孩子设为空，代表已访问其右孩子
            root.rchild = NULL;       
            pop(&bs);
            push(&bs, root);
            //右孩子入栈
            root = *temp;      
            push(&bs, root);
            //'1'入字符栈
            charPush(&cs, '1');
        }    
    }
}

　　（5）解码

'''C
char stack[7][10];             //记录a~g的编码
//遍历栈，得到字符c的编码
void traverseStack(charStack s, char c)
{
    int index = c - 'a'; 
    int i = 0;
    while(s.base != s.top)
    {
        stack[index][i] = *s.base;
        i++;
        s.base++;
    }
}
 
 
//通过哈夫曼树编码
void encodeHuffman(Tree T)
{  
    BiStack bs = stackInit();
    charStack cs = charStackInit();
    Huffman root = *T;  
    Tree temp = NULL;
    push(&bs, root);      //根结点入栈
    while(bs.top != bs.base)      //栈空表示遍历结束
    {
        root = getTop(bs);
        temp = root.lchild;       //先访问左孩子
        while(temp != NULL)       //左孩子不为空
        {
            //将结点左孩子设为空，代表已访问其左孩子
            root.lchild = NULL;
            pop(&bs);            
            push(&bs, root);
            //左孩子入栈
            root = *temp;
            temp = root.lchild;
            push(&bs, root);
            //'0'入字符栈
            charPush(&cs, '0');
        }
        temp = root.rchild;     //后访问右孩子     
        while(temp == NULL)     //右孩子为空，代表左右孩子均已访问，结点可以出栈 
        {
            //结点出栈
            root = pop(&bs);
            //寻到叶子结点，可以得到结点中字符的编码
            if(root.c != ' ')
                traverseStack(cs, root.c);
            charPop(&cs);       //字符栈出栈
            if(bs.top == bs.base) break;    //根结点出栈，遍历结束
            //查看上一级结点是否访问完左右孩子  
            root = getTop(bs);
            temp = root.rchild;           
        }
        if(bs.top != bs.base)
        {
            //将结点右孩子设为空，代表已访问其右孩子
            root.rchild = NULL;       
            pop(&bs);
            push(&bs, root);
            //右孩子入栈
            root = *temp;      
            push(&bs, root);
            //'1'入字符栈
            charPush(&cs, '1');
        }    
    }
}

　　（6）主函数

'''C
void main()
{
    pList pl = creatList();
    printf("字符的权重如下\n");
    for(pList l = pl; l->next != NULL; l = l->next)
        printf("字符%c的权重是 %d\n", l->root->c, l->root->weight);
    Tree T = creatHuffman(pl);
    encodeHuffman(T);
    printf("\n\n字符编码结果如下\n");
    for(int i = 0; i < 7; i++)
        printf("%c : %s\n", i+'a', stack[i]);
    char code[100];
    printf("\n\n请输入编码：\n");
    scanf("%s", code);
    printf("解码结果如下：\n");
    decodeHuffman(T, code);
    printf("%s\n", decode);
    printf("\n\n");
    system("date /T");
    system("TIME /T");
    system("pause");
    exit(0); 
}

　　2、运转答案如下：

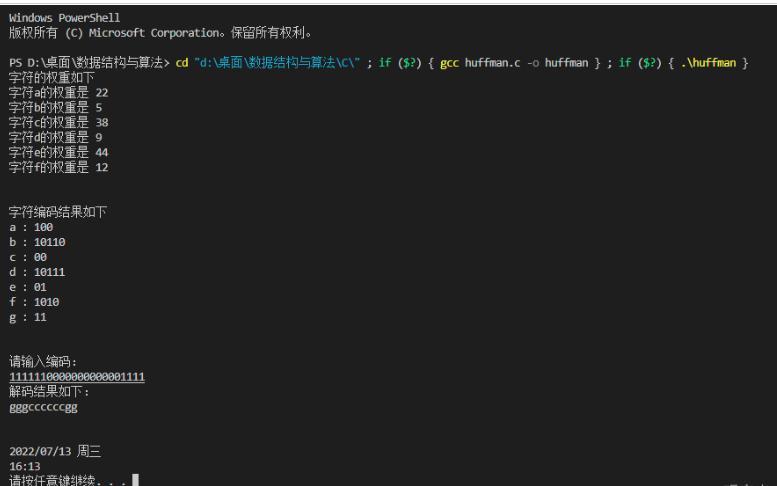
　　二、实现Python功能

　　1、代码解释

　　（1）创建哈夫曼树

#coding=gbk
 
import datetime
import time
from pip._vendor.distlib.compat import raw_input
 
#哈夫曼树结点类
class Huffman:
    def __init__(self, c, weight):
        self.c = c
        self.weight = weight
        self.lchild = None
        self.rchild = None
    
    #创建结点左右孩子    
    def creat(self, lchild, rchild):
        self.lchild = lchild
        self.rchild = rchild
 
#创建列表        
def creatList():
    list = []
    list.append(Huffman('a', 22))
    list.append(Huffman('b', 5))
    list.append(Huffman('c', 38))
    list.append(Huffman('d', 9))
    list.append(Huffman('e', 44))
    list.append(Huffman('f', 12))
    list.append(Huffman('g', 65))
    return list
 
#通过列表创建哈夫曼树，返回树的根结点
def creatHuffman(list):
    while len(list) > 1:               #列表只剩一个结点时循环结束，此结点即为哈夫曼树的根结点
        i = 0
        j = 1
        k = 2
        while k < len(list):           #找到列表中权重最小的两个结点list1,list2          
            if list[i].weight > list[k].weight or list[j].weight > list[k].weight:
                if list[i].weight > list[j].weight:
                    i = k
                else:
                    j = k
            k += 1       
        root = Huffman(' ', list[i].weight + list[j].weight) #新结点字符统一设为空格，权重设为list1与list2权重之和   
        if list[i].weight < list[j].weight:                  #list1和list2设为新结点的左右孩子
            root.creat(list[i], list[j])
        else:
            root.creat(list[j], list[i])
        #list1数据域替换成新结点，并删除list2
        list[i] = root
        list.remove(list[j])
    return list[0]

　　（2）编码

#通过哈夫曼树编码
def encodeHuffman(T):
    code = [[], [], [], [], [], [], []]
    #列表实现栈结构
    treeStack = []
    codeStack = []
    treeStack.append(T)
    while treeStack != []:        #栈空代表遍历结束
        root = treeStack[-1]
        temp = root.lchild
        while temp != None:
            #将结点左孩子设为空，代表已访问其左孩子
            root.lchild = None        
            #左孩子入栈          
            treeStack.append(temp)         
            root = temp
            temp = root.lchild
            #0入编码栈
            codeStack.append(0)
        temp = root.rchild            #后访问右孩子
        while temp == None:           #右孩子为空，代表左右孩子均已访问，结点可以出栈
            root = treeStack.pop()           #结点出栈
            #寻到叶子结点，可以得到结点中字符的编码
            if root.c != ' ':
                codeTemp = codeStack.copy()
                code[ord(root.c) - 97] = codeTemp     
            if treeStack == []:    #根结点出栈，遍历结束
                break
            codeStack.pop()        #编码栈出栈
            #查看上一级结点是否访问完左右孩子
            root = treeStack[-1]
            temp = root.rchild
        if treeStack != []:
            treeStack.append(temp)     #右孩子入栈
            root.rchild = None         #将结点右孩子设为空，代表已访问其右孩子
            codeStack.append(1)        #1入编码栈
    return code

　　（3）解码

#通过哈夫曼树解码
def decodeHuffman(T, strCode):
    decode = []
    index = 0
    while index < len(strCode):        #01编码字符串读完，解码结束
        root = T
        while root.lchild != None:     #找到叶子结点
            if index < len(strCode):
                if strCode[index] == '0':
                    root = root.lchild
                else:
                    root = root.rchild
                index += 1
            else:
                break
        decode.append(root.c)           #叶子结点存放的字符即为解码得到的字符
    return decode

　　（4）主函数

if __name__ == '__main__':
    list = creatList()
    print("字符的权重如下")
    for i in range(len(list)):
        print("字符{}的权重为: {}".format(chr(i+97), list[i].weight))
    T = creatHuffman(list)
    code = encodeHuffman(T)
    print("\n字符编码结果如下")
    for i in range(len(code)):
        print(chr(i+97), end=' : ')
        for j in range(len(code[i])):
            print(code[i][j], end='')
        print("")
    strCode = input("\n请输入编码：\n")
    #哈夫曼树在编码时被破坏，必须重建哈夫曼树
    list = creatList()
    T = creatHuffman(list)
    decode = decodeHuffman(T, strCode)
    print("解码结果如下：")
    for i in range(len(decode)):
        print(decode[i], end='')
    print("\n\n")
    datetime = datetime.datetime.now()
    print(datetime.strftime("%Y-%m-%d\n%H:%M:%S"))
    input("Press Enter to exit…")

　　2、运行结果

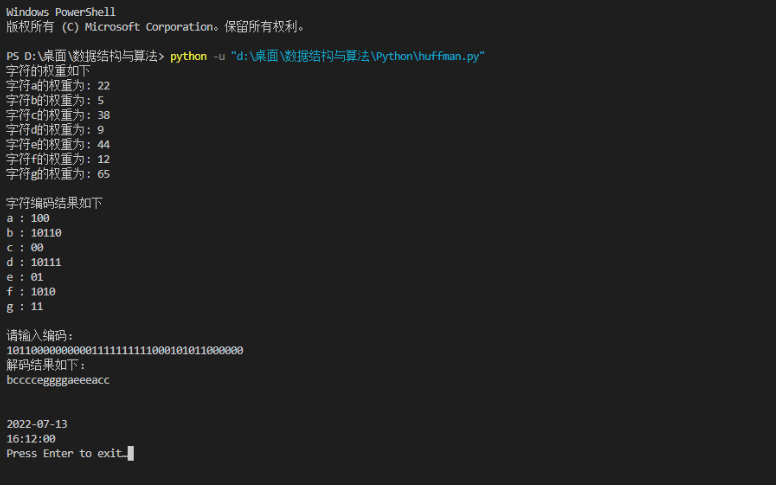
　　以上就是关于哈夫曼编码的相关介绍，希望可以为各位读者带来一定的帮助。。

GPU云服务器云服务器霍夫曼树编码c语言 n元霍夫曼编码c语言哈夫曼编码哈夫曼算法压缩c语言

文章版权归作者所有，未经允许请勿转载,若此文章存在违规行为，您可以联系管理员删除。

转载请注明本文地址：https://www.ucloud.cn/yun/127609.html

数据结构：哈夫曼编码（php版）

摘要：在计算机信息处理中，哈夫曼编码是一种一致性编码法又称熵编码法，用于数据的无损耗压缩。构造树时间复杂度选择两个使用频率较小字符在字符串中出现的次数的结点合并生成出一个树循环创建哈夫曼树数组函数删除数组中的第一个元素，并返回被删除元素的值。小草主要博客：http://homeway.me/ 演示网址：http://huffman.sinaapp.com/ 源文件下载地址：http:...

luodongseu 2019-06-27 10:32 评论0 收藏0

发表评论

登陆后可评论

0条评论

89542767

男|高级讲师

我要关注我要私信

TA的文章

pythontime控制模块时间格式与结构型时长详细说明

阅读 889·2023-01-14 11:38
OpenMV与JSON编码问题分析

阅读 833·2023-01-14 11:04
python中的特性管理模式详细说明

阅读 684·2023-01-14 10:48
Python运用fastapi完成上传图片

阅读 1887·2023-01-14 10:34
pythonopencv图象高通滤波和低通滤波器的范例编码

阅读 891·2023-01-14 10:24
Python根据ssh远程桌面连接Mysql数据库操作

阅读 750·2023-01-14 10:18
本文轻轻松松掌握Python中类的继承

阅读 479·2023-01-14 10:09
python中wordcloud组装方式总结

阅读 519·2023-01-14 10:02

资讯专栏INFORMATION COLUMN

上云采购季！| 2核2G4M爆款云服务器低至59元/年，更有多台、长期优惠，快来选购！

怎么利用Python和C语言实现哈夫曼编码（霍夫曼编码）

相关文章

**数据结构：哈夫曼编码（php版）**

发表评论

0条评论

89542767

男|高级讲师

TA的文章

pythontime控制模块时间格式与结构型时长详细说明

OpenMV与JSON编码问题分析

python中的特性管理模式详细说明

Python运用fastapi完成上传图片

pythonopencv图象高通滤波和低通滤波器的范例编码

Python根据ssh远程桌面连接Mysql数据库操作

本文轻轻松松掌握Python中类的继承

python中wordcloud组装方式总结

最新活动