摘要:列生成是用于求解大规模线性优化问题的一种算法,其实就是单纯形法的一种形式。如果需要求得整数最优解需要结合分支定界算法。子问题用于生成新的切割方案列,子问题的约束对应切割约束。
列生成是用于求解大规模线性优化问题的一种算法,其实就是单纯形法的一种形式。单纯性可以通过不断迭代,通过换基变量的操作,最终找到问题的最优解。但是当问题的规模很大之后,变量的个数就会增大到在有限时间内无法有效迭代求解。所以可以用列生成方法求解,列生成方法可以一开始不列举所有的列,通过不断给模型中加入列的方式,最终找到全部解,其关键点就是加新列的过程,可以只加入能让目标值更优的列,从而减少变量的使用个数。
列生成算法流程
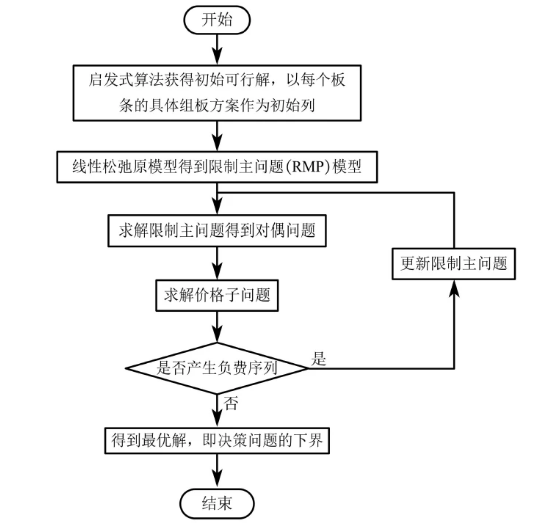
列生成过程中,需要将问题建模为主问题+子问题的形式。
主问题:就是原问题,主要用于决策是否选用某些方案(列)
主问题松弛问题:将主问题变量范围正整数松弛到正数
限制主问题:主问题去掉一部分列
限制主问题对偶问题:对限制主问题求对偶
价格子问题:原问题的局部问题,用于生成新的方案(列)
求解Cutting Stock问题
问题描述:
将一些钢管切割成为需要的长度以满足客户需求,要求使用的钢管最少。
每根钢管长度L=16m
需求:3m钢管25根;6m钢管20根,7米钢管18根
模型建立
主问题
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /in Z /qquad /qquad /quad /forall j /in J /]
/(x_j/): 方案选用的个数
/(a_{ij}/): 方案/(j/)中钢管/(i/)的个数
/(d_i/): 钢管/(i/)的需求量
主问题松弛问题
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /ge 0 /qquad /qquad /quad /forall j /in J /]
变量是整数的情况下无法用列生成法求得最优解,需要将问题松弛。如果需要求得整数最优解需要结合分支定界算法。
限制主问题
/[min/sum_{j /in J} x_{j}//s.t./qquad/qquad/qquad/qquad/qquad///sum_{j /in J} x_j a_{ij} /ge d_i /qquad /forall i /in I//x_j /ge 0 /qquad /qquad /quad /forall j /in /Omega_j /]
将主问题中的变量规模减小,一开始只加入一部分可行的切割方案(/(a_j/),列),列生成就是不断生成新的/(a_j/) 加入到问题中。判断一个列是否可以加入到问题,需要判断检验数/(/sigma_j = c_j - c_B B^{-1}a_j/),如果检验数为负,就可以将新的列加入。其中/(c_BB^{-1}/)有两重含义:
- 通过限制主问题求得的影子价格
- 通过限制主问题求得的对偶变量
对偶问题和原问题有同样的最优解,将原问题进行对偶,可以把原问题的变量转化为约束、约束转化为变量,因此,对于变量很多的问题将其转化为对偶问题可以很容易得到其子问题。
对偶问题
/[max /sum_{i /in I} d_i v_i //s.t./qquad/qquad/qquad/qquad/qquad///sum_{i in / I} a_{ij} v_i /le 1 /qquad /qquad /forall j /in /Omega_j //v_j /ge 0 /qquad /qquad /qquad /quad/forall i /in I /]
对偶问题用于推导子问题。可以进入主问题的列,就是检验数为负数的列,对于对偶问题,就是违反了约束的列。对偶问题中只有一个约束,/(/sum_{i in / I} a_{ij} /lambda_i /le 1/)可以写成/(1-/sum_{i /in I} a_i /lambda_i /ge 0/),求其最小值,如果最小值小于0,则说明其违反了约束。子问题用于生成新的切割方案(列),子问题的约束对应切割约束。
子问题
/[min /quad 1-/sum_{i /in I} a_i v_i //s.t./qquad/qquad/qquad/qquad/qquad///sum_{i /in I} a_i l_i /le L /qquad /forall i /in I //a_i /ge 0 /qquad /quad /quad /forall i /in I /]
数据带入模型
以下所有的求解都可以用CPLEX进行求解,直接用CPLEX IDE实现
1. 启发式获得初始切割方案
首先有可行的切割方案才能构造出主问题,因此可以用启发式先计算出一些可行的切割方案,用于构造主问题。很简单的,每根钢管只生产一种产品,可以得到三种切割方案
2.开始列生成迭代
第1次迭代
松弛限制主问题:
/[min /quad x_1 + x_2 + x_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad /ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad /ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad/ge 18 // /quad/quad/quad x_1,/quad x_2,/quad x_3 /quad /ge 0 /]
对偶问题:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 // /quad/quad /quad v_1,/quad /quad v_2,/quad /quad v_3 /quad /ge 0 /]
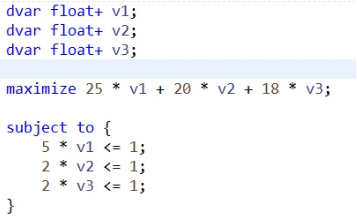

求得对偶变量的值,将其带入到子问题中
子问题:
/[min /quad 1-0.2a_1-0.5a_2-0.5a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

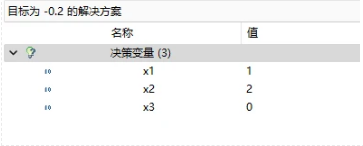
目标函数值为-0.2<0,可以加入到主问题中继续求解,新加入的一列是/(a_4=[1,2,0]^T/),表示这个方案中一根钢管切出一根3m和2根6米
第2次迭代
松弛限制主问题:
/[min /quad x_1 + x_2 + x_3 + x_4 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad + x_4 /quad/ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad + 2x_4 /ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad /quad/quad/quad/ge 18 // /quad/quad/quad x_1,/quad x_2,/quad x_3, /quad x_4 /quad /ge 0 /]
对偶问题:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 ///qquad /quad v_1/quad+2v_2 /quad/quad/quad/quad/le 1 // /quad/quad /quad v_1, /qquad v_2, /qquad v_3 /quad /ge 0 /]
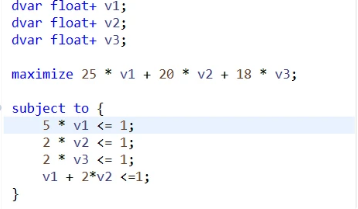
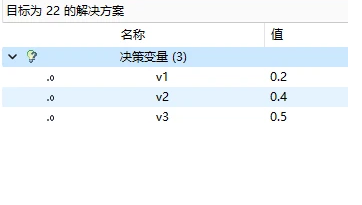
求得对偶变量的值,将其带入到子问题中
子问题:
/[min /quad 1-0.2a_1-0.4a_2-0.5a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

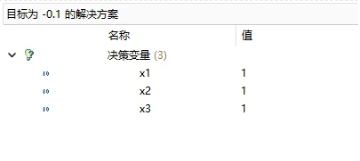
目标函数值为-0.1<0,可以加入到主问题中继续求解,可以加入到主问题中继续求解,新加入的一列是/(a_4=[1,1,1]^T/),表示这个方案中一根钢管切出1根3m,1根6米,1根7米
第3次迭代
松弛限制主问题:
/[min /quad x_1 + x_2 + x_3 + x_4 + x_5//s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad5x_1 /qquad /qquad /quad + x_4 /quad + x_5/ge 25 ///quad/quad/quad/qquad 2x_2 /qquad /quad + 2x_4 +x_5/ge 20 ///quad/quad/quad/qquad /qquad 2x_3 /quad /quad/quad/quad +x_5/ge 18 // /quad/quad x_1,/quad x_2,/quad x_3, /quad x_4, /quad x_5 /quad/quad/ge 0 /]
对偶问题:
/[max /quad 25 v_1 + 20 v_2 + 18v_3 //s.t./qquad/qquad/qquad/qquad/qquad///qquad /quad 5v_1 /qquad /qquad /qquad /quad/le 1 ///qquad /quad/qquad /quad 2v_2 /qquad /quad /quad/le 1 ///qquad /quad/qquad /qquad /qquad 2v_3/quad /le 1 ///qquad /quad v_1/quad+2v_2 /quad/quad/quad/quad/le 1 // /qquad /quad v_1/quad+v_2/quad+v_3 /quad/le 1 ///quad/quad /quad v_1, /qquad v_2, /qquad v_3 /quad /ge 0 /]
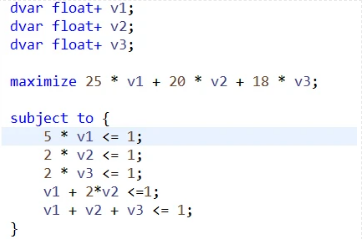
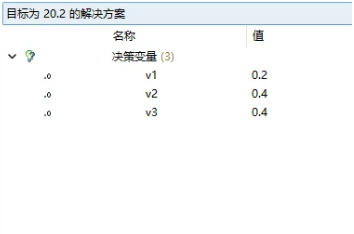
求得对偶变量的值,将其带入到子问题中
子问题:
/[min /quad 1-0.2a_1-0.4a_2-0.4a_3 //s.t./qquad/qquad/qquad/qquad/qquad///quad/quad/quad 3a_1+6a_2+7a_3 /le 16///quad/quad/quad a_1, /quad a_2, /quad a_3 /quad /ge 0 /]

根据求解可以得到
目标值:20.2
切割方案:方案1选择1.2个;方案4选择1个,方案5选择18个
最后求得的结果包含了小数,如果想要取得整数解,需要结合分支定界算法













